Department do

Decision and Optimization

The "Decision and Optimization" department develops theoretical and methodological contributions for the design of mathematical laws and algorithmic techniques dedicated to control and decision problems.


head

Dmitry Peaucelle

Methodologies

Methodologies are the core of the research in the DO department. In 2019, we identified six topics that illustrate the common features of our activities:

  • certificates
  • hierarchies
  • uncertainties
  • computational methods
  • codes and applications
  • international cooperation and LAAS-DO Fellows

The topics express the continuum of activities from theoretical results to software products. Most of the DO contributions borrow to more than one of these topics. We for example aim at systematically provide efficient algorithmic or numerical tools for solving generic problems. Conversely, theoretical results are formulated in such a manner that tools, mainly optimization based, car be used. Theory is considered with the aim of leading to practical solutions for applications from industrial and other partners. We cherish doing this research work with many colleagues from abroad who bring us fruitful alternative view points on the considered topics.

The papers cited in the following are illustrative of the topics and constitue a partial coverage of the results published before 2019.

Certificates

Reliable Decision and Optimization requires guaranteed properties such as stability, performance, robustness, security, tolerance, convergence, reduced error bounds, etc. Such properties are hard and often impossible to compute directly or analytically. The approach in the DO department consist of producing indirect means to guarantee related quantities of the considered properties. These means are gathered under the naming of Certificates: mathematical or algorithmic objects providing guarantees. We distinguish among the certificates those on solutions (existence/characterization) ; those on asymptotic behavior (stability and others) ; those for constraint satisfaction ; those for measuring complexity.

Some results in terms of Certificates:

Hierarchies

Performances (stability, bounds on energies) of engineering systems are recast as decision problems (satisfaction of contraints, optimization) which by default are hard (infinite dimensional, non-linear, non-convex). To circumvent the difficulties, DO develops hierarchies of simpler problems (finite dimensional, linear or convex) whose solutions may converge in some sense to the solution of the original problem. Convergent or complete hierarchies are such that the sequence of relaxed problems grow in size (number of decision variables and contraints) with respect to some relaxation index (for example the degree of involved polynomials) and as the index grows to infinity the relaxed evaluation converges to the exact value of the performance. Incomplete hierarchies are those for which convergence is experimentally verified but not formally proven.

Some results in terms of Certificates:

Uncertainties

Uncertainties are considered in the context of feedback control, parameter estimation and diagnosis of dynamical systems, continuous and combinatorial optimization. The uncertainty sets are described by one or several mathematical models among intervals, zonotopes, polytopes as well as described by bounded norms, weighted or not. The goal is to evaluate the effect of the uncertainties on the to be measured performances which themselves happen to lie in a variety of sets.

Some results in terms of Uncertainties:

Computational methods

The researchers of the department conceive efficient concrete algorithmic methods. These have provided significant progress if the Control, AI and Operational Research fields. The three main topics for which contributions were provided are optimization, diagnosis and control, learning.

Some results in terms of Computational methods:

Codes and applications

The DO department produces various codes and softwares. Software are intended to promote generic solutions. These are distributed in most of the cases in open access and some have benefited of maturation transfer processes. The codes are produced more specifically for concrete applications in cooperation with industrial partners.

2019 report

in 2019 the department produced a report of 2015-2019 activities and prospectives for 2020-2025.

International cooperation

The DO department cherishes international cooperation. It is attested by the reputation indicators of the teams (DISCO, MAC, POP, ROC) and also by the many foreign PhD students and temporary researchers hosted in the department.

Staring from 2021 the DO-LAAS department (Decision and Optimization) acknowledges fellow colleagues from abroad who collaborate closely with members of the department. The eligible colleagues should be members of research institutions in a foreign country, should have visited or stayed at LAAS in Toulouse in the previous five years, and have co-signed scientific results with DO-LAAS members. Nominations are made by DO-LAAS members. The DO-LAAS scientific council validates and the head of the department appoints the DO-LAAS Research Fellows.

2023 DO-LAAS Research Fellows

2021 DO-LAAS Research Fellows

AREAS OF

RESEARCH AND APPLICATIONS

DO activities focus and classes of models and data, on generic optimization and decision problems. Meanwhile and therefore, the considered applications are various in type and concern diverse industries and services.

DISCIPLINARY FIELDS

COVERED IN OUR DEPARTMENT

DEPARTMENT TEAMS

All four teams combine both decision and optimization topics. POP and ROC focus on (polynomial and combinatorial) optimization and consider its usage in on decision making. DISCO and MAC focus on decision design (diagnosis and control) often based on optimization tools.

Un stéthoscope apposé sur un clavier oscultant ainsi l'état de santé de l'ordinateur

disco

Yannick Pencole

The DISCO team conducts broad-spectrum methodological research in the field of diagnostics and health monitoring of complex systems, a research theme at the frontier between Automatic Control and Artificial Intelligence.

+

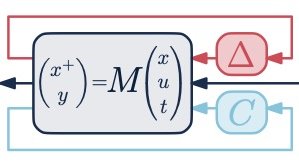
LogoMAC

mac

Lucie Baudouin

The MAC Team does research in the field of systems and control theory. We develop a mathematical and theoretical basis for dynamical systems control, including modeling, design, analysis and optimization.

+

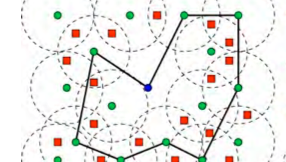
Optimisation Combinatoire

roc

Laurent Houssin

Team ROC works on combinatorial optimisation problems, and on the algorithmic methods to solve them, bridging Operations Research and Artificial Intelligence.

+

Polynomial

pop

Victor Magron

The POP team focuses on solving notoriously difficult and non-convex polynomial optimization problems, arising from several adjacent fields.

+

Latest publications

2025

Journal articles

Shenyu Liu, Aneel Tanwani. Impulsive switching signals with functional inequalities: Stability analysis using hybrid systems framework. Automatica, 2025, 171, pp.111928. ⟨10.1016/j.automatica.2024.111928⟩. ⟨hal-04707528⟩

Aneel Tanwani, Hyungbo Shim, Andrew Teel. Singularly Perturbed Hybrid Systems for Analysis of Networks with Frequently Switching Graphs. IEEE Transactions on Automatic Control, 2025, 70 (7), pp.1 - 16. ⟨10.1109/TAC.2024.3523242⟩. ⟨hal-04855233⟩

Matteo Della Rossa, Aneel Tanwani. Converse Lyapunov Results for Stability of Switched Systems with Average Dwell-Time. ESAIM: Control, Optimisation and Calculus of Variations, In press. ⟨hal-04616636⟩

Muhammad Zaki Almuzakki, Bayu Jayawardhana, Aneel Tanwani, Antonis Vakis. Exponential stabilization of linear systems using nearest-action control with countable input set. Systems and Control Letters, 2025, 196, pp.105992. ⟨10.1016/j.sysconle.2024.105992⟩. ⟨hal-04826783⟩

Xavier Allamigeon, Stéphane Gaubert, Ricardo Katz, Mateusz Skomra. Universal complexity bounds based on value iteration for stochastic mean payoff games and entropy games. Information and Computation, 2025, 302, pp.105236. ⟨10.1016/j.ic.2024.105236⟩. ⟨hal-04859637⟩

Conference papers

Tanguy Terrien, Cyrille Briand, Philippe Truillet. Preemptive shift-based scheduling with maximum workload constraints. ROADEF 2025, Feb 2025, Champs-sur-Marne, France. ⟨hal-04832630⟩

Preprints, Working Papers, ...

Marco Sterlini, Samuele Zoboli, Sophie Tarbouriech. Layer-wise dynamic event-triggered neural network control for discrete-time nonlinear systems. 2025. ⟨hal-04870932⟩

Víctor Blanco, Victor Magron, Miguel Martínez-Antón. On the Complexity of p-Order Cone Programs. 2025. ⟨hal-04896611⟩

Jean B Lasserre. Rank conditions for exactness of semidefinite relaxations in polynomial optimization. 2025. ⟨hal-04877125⟩

Igor Klep, Victor Magron, Jurij Volčič. Complete Upper Bound Hierarchies for Spectral Minimum in Noncommutative Polynomial Optimization. 2025. ⟨hal-04875437⟩

2024

Journal articles

Matthieu Masson, Denis Arzelier, Florent Bréhard, Mioara Joldes, Bruno Salvy. Fast and reliable computation of the instantaneous orbital collision probability. Journal of Guidance, Control, and Dynamics, 2024, pp.1-14. ⟨10.2514/1.G008102⟩. ⟨hal-04134188⟩

Idir Hamaz, Laurent Houssin, Sonia Cafieri. The robust cyclic job shop problem. European Journal of Operational Research, 2024, 312 (3), pp.855-865. ⟨10.1016/j.ejor.2023.07.042⟩. ⟨hal-03683608v2⟩

Renjie Ma, Zhijian Hu. Deep Neural Network-Controlled Safety-Critical Systems With Uncertainty Resilience. IEEE Internet of Things Journal, 2024, 11 (13), pp.24061 - 24072. ⟨10.1109/jiot.2024.3389458⟩. ⟨hal-04555816⟩

Nicolas Augier, Didier Henrion, Milan Korda, Victor Magron. Symmetry reduction and recovery of trajectories of optimal control problems via measure relaxations. ESAIM: Control, Optimisation and Calculus of Variations, 2024, 30, pp.63. ⟨10.1051/cocv/2024053⟩. ⟨hal-04694171v2⟩

Carla de Souza, Sophie Tarbouriech, Isabelle Queinnec, Antoine Girard. Nonstandard anti-windup approach for event-triggered control purpose. Systems and Control Letters, 2024, 185, pp.105715. ⟨10.1016/j.sysconle.2024.105715⟩. ⟨hal-04378600⟩

Florent Koudohode, Nicolás Espitia, Miroslav Krstic. Event-triggered boundary control of an unstable reaction diffusion PDE with input delay. Systems and Control Letters, 2024, 186. ⟨hal-04304378⟩

Nicola Zaupa, Giulia Giordano, Isabelle Queinnec, Sophie Tarbouriech, Luca Zaccarian. Equivalent Conditions for the Synchronization of Identical Linear Systems over Arbitrary Interconnections. European Journal of Control, 2024, 80 (Part B), pp.101099. ⟨10.1016/j.ejcon.2024.101099⟩. ⟨hal-04359774v2⟩

Florent Bréhard, Nicolas Brisebarre, Mioara Joldeş, Warwick Tucker. Efficient and Validated Numerical Evaluation of Abelian Integrals. ACM Transactions on Mathematical Software, 2024, 50 (1), pp.1 - 38. ⟨10.1145/3637550⟩. ⟨hal-03561096v2⟩

Tom Portoleau, Christian Artigues, Romain Guillaume. Robust decision trees for the multi-mode project scheduling problem with a resource investment objective and uncertain activity duration. European Journal of Operational Research, 2024, 312 (2), pp.525-540. ⟨10.1016/j.ejor.2023.07.035⟩. ⟨hal-03502505⟩

Jie Wang, Jacopo Surace, Irénée Frérot, Benoît Legat, Marc-Olivier Renou, et al.. Certifying ground-state properties of many-body systems. Physical Review X, 2024, 14 (3), pp.031006. ⟨10.1103/PhysRevX.14.031006⟩. ⟨hal-04264341⟩

Jean-Bernard Lasserre. Gaussian mixtures closest to a given measure via optimal transport. Comptes Rendus. Mathématique, 2024, 362, pp.1455-1473. ⟨10.5802/crmath.657⟩. ⟨hal-04560365⟩

Marc Dambrine, Ch Dossal, Bénédicte Puig, Aude Rondepierre. Stochastic Differential Equations for modeling first order optimization methods. SIAM Journal on Optimization, 2024, 34 (2). ⟨hal-03630785v2⟩

Tamara Borreguero Sanchidrián, Tom Portoleau, Christian Artigues, Alvaro García Sánchez, Miguel Ortega Mier, et al.. Large neighborhood search for an aeronautical assembly line time-constrained scheduling problem with multiple modes and a resource leveling objective. Annals of Operations Research, 2024, 338 (1), pp.13-40. ⟨10.1007/s10479-023-05629-3⟩. ⟨hal-04229939⟩

Carine Jauberthie, Nathalie Verdière, Louise Travé-Massuyès. Functional Diagnosability of Possibly Uncertain Systems. IEEE Control Systems Letters, 2024, 8, pp.2181-2186. ⟨10.1109/LCSYS.2024.3456230⟩. ⟨hal-04703936⟩

Jean-Bernard Lasserre, Yuan Xu. A Generalized Pell's equation for a class of multivariate orthogonal polynomials. Transactions of the American Mathematical Society, In press, 23 p. ⟨10.1090/tran/9200⟩. ⟨hal-04163153v2⟩

Philipp Braun, Giulia Giordano, Christopher M. Kellett, Iman Shames, Luca Zaccarian. Optimizing shifted stabilizers with asymmetric input saturation. IEEE Transactions on Automatic Control, In press, ⟨10.1109/TAC.2024.3436728⟩. ⟨hal-03586545v2⟩

Edgar Hernando Sepúlveda-Oviedo, Louise Travé-Massuyès, Audine Subias, Marko Pavlov, Corinne Alonso. An ensemble learning framework for snail trail fault detection and diagnosis in photovoltaic modules. Engineering Applications of Artificial Intelligence, 2024, 137 (Part A), pp.109068. ⟨10.1016/j.engappai.2024.109068⟩. ⟨hal-04689176⟩

Simone Mariano, Romain Postoyan, Luca Zaccarian. Finite-time stability properties of Lur'e systems with piecewise continuous nonlinearities. IEEE Transactions on Automatic Control, 2024, 69 (9), pp.6325-6332. ⟨10.1109/TAC.2024.3383278⟩. ⟨hal-04530198⟩

Mathieu Bajodek, Hugo Lhachemi, Giorgio Valmorbida. Necessary stability conditions for reaction-diffusion-ODE systems. IEEE Transactions on Automatic Control, 2024, 69 (11), pp.1-8. ⟨10.1109/TAC.2024.3407818⟩. ⟨hal-04008999⟩

Carolina Albea, Mathias Serieye, Alexandre Seuret, Marc Jungers. Stabilization of aperiodic sampled-data switched affine systems to hybrid limit cycles. European Journal of Control, 2024, 79, pp.101094. ⟨10.1016/j.ejcon.2024.101094⟩. ⟨hal-04814278⟩

Francesco Ferrante, Sophie Tarbouriech. Sampled-data feedback control design in the presence of quantized actuators. Nonlinear Analysis: Hybrid Systems, 2024, 54, pp.101530. ⟨10.1016/j.nahs.2024.101530⟩. ⟨hal-04687532⟩

Edgar Hernando Sepúlveda-Oviedo, Leonardo Enrique Bermeo Clavijo, Luis Carlos Méndez-Córdoba. Effect of timing of umbilical cord clamping and birth on fetal to neonatal transition: OpenModelica-based virtual simulator-based approach. Biocybernetics and Biomedical Engineering, 2024, 44 (3), pp.716-730. ⟨10.1016/j.bbe.2024.08.008⟩. ⟨hal-04687787⟩

Jean-Bernard Lasserre. The Moment-SOS hierarchy: Applications and related topics. Acta Numerica, 2024, 33, pp.841-908. ⟨10.1017/S0962492923000053⟩. ⟨hal-04687963⟩

Zhijian Hu, Qingyang Li, Pu Zhang, Ruiping Wang, Kai Zhang. A Novel Handling Method to Intermittent Feedback in Load Frequency Regulation for Renewable Energy-Dominated Microgrids. IEEE Transactions on Instrumentation and Measurement, 2024, 73, ⟨10.1109/TIM.2024.3457958⟩. ⟨hal-04732942⟩

Kai Zhang, Meilin Li, Zhijian Hu, Xuefei Yang, Kang-Kang Zhang. Periodic Event-Triggered and Self-Triggered Control of Spacecraft Rendezvous System With Input Delay. IEEE Transactions on Automation Science and Engineering, 2024, pp.1-9. ⟨10.1109/TASE.2024.3439009⟩. ⟨hal-04675551⟩

Adrien Le Franc, Victor Magron, Jean-Bernard Lasserre, Manuel Ruiz, Patrick Panciatici. Minimal Sparsity for Second-Order Moment-SOS Relaxations of the AC-OPF Problem. IEEE Transactions on Power Systems, 2024, 39 (3), pp.5408 - 5415. ⟨10.1109/TPWRS.2023.3333691⟩. ⟨hal-04110742v2⟩

Mathieu Bajodek, Alexandre Seuret, Frédéric Gouaisbaut. On the necessity of sufficient LMI conditions for time-delay systems arising from Legendre approximation. Automatica, 2024, 159, pp.111322. ⟨10.1016/j.automatica.2023.111322⟩. ⟨hal-03435008v3⟩

Riccardo Bertollo, Michael Schwegel, Andreas Kugi, Luca Zaccarian. Integrate-and-Reset Feedback and Feedforward for a Solenoid With Unknown Parameters. IEEE Control Systems Letters, 2024, 8, pp.1511-1516. ⟨10.1109/LCSYS.2024.3413360⟩. ⟨hal-04776122⟩

Ophélie Thomas- -Chemin, Childérick Séverac, Abderazzak Moumen, Adrian Martinez Rivas, Christophe Vieu, et al.. Automated bio-AFM generation of large mechanome data set and their analysis by machine learning to classify cancerous cell lines. ACS Applied Materials & Interfaces, 2024, 16 (34), pp.44504-44517. ⟨10.1021/acsami.4c09218⟩. ⟨hal-04674006⟩

Joseph Breeden, Luca Zaccarian, Dimitra Panagou. Robust Safety-Critical Control for Systems With Sporadic Measurements and Dwell Time Constraints. IEEE Control Systems Letters, 2024, 8, pp.1415 - 1420. ⟨10.1109/LCSYS.2024.3410631⟩. ⟨hal-04605927⟩

Benoît Bonnet-Weill, Hélène Frankowska. On the Viability and Invariance of Proper Sets under Continuity Inclusions in Wasserstein Spaces. SIAM Journal on Mathematical Analysis, 2024, 56 (3), pp.2863-2914. ⟨10.1137/23M1560410⟩. ⟨hal-04082985v2⟩

Yohei Hosoe, Yuki Michitani, Dimitri Peaucelle, Tomomichi Hagiwara. Stochastic Gain-Scheduled Control of Discrete-Time Systems Characterized by Random Polytopes. IEEE Control Systems Letters, 2024, 8, pp.229 - 234. ⟨10.1109/LCSYS.2024.3366179⟩. ⟨hal-04448570⟩

Benoît Bonnet-Weill, Hélène Frankowska. Carathéodory Theory and A Priori Estimates for Continuity Inclusions in the Space of Probability Measures. Nonlinear Analysis: Theory, Methods and Applications, 2024, 247, pp.113595. ⟨10.1016/j.na.2024.113595⟩. ⟨hal-03969118v2⟩

Andrea Cristofaro, Luca Zaccarian. Adaptive Pseudoinverse Observers for Output Redundant Discrete-Time Linear Systems. IEEE Transactions on Automatic Control, 2024, 69 (11), pp.7403-7417. ⟨10.1109/TAC.2024.3388129⟩. ⟨hal-04776114⟩

Philipp Braun, Abhishek Bhardwaj, Mirko Brentari, Luca Zaccarian, Matteo Saveriano. Static anti-windup with shifted equilibria applied to a Segway-like vehicle. Automatica, 2024, 169, pp.111830. ⟨10.1016/j.automatica.2024.111830⟩. ⟨hal-04776120⟩

Alessandro Bosso, Ilario Azzollini, Simone Baldi, Luca Zaccarian. Adaptive Hybrid Control for Robust Global Phase Synchronization of Kuramoto Oscillators. IEEE Transactions on Automatic Control, 2024, 69 (12), pp.8188 - 8203. ⟨10.1109/TAC.2024.3403692⟩. ⟨hal-04776121⟩

Riccardo Ballaben, Philipp Braun, Luca Zaccarian. Lyapunov-Based Avoidance Controllers With Stabilizing Feedback. IEEE Control Systems Letters, 2024, 8, pp.862-867. ⟨10.1109/LCSYS.2024.3404770⟩. ⟨hal-04776123⟩

Mattia Giaccagli, Samuele Zoboli, Daniele Astolfi, Vincent Andrieu, Giacomo Casadei. Synchronization in networks of nonlinear systems: Contraction analysis via Riemannian metrics and deep-learning for feedback estimation. IEEE Transactions on Automatic Control, 2024, 69 (11), pp.8041-8048. ⟨10.1109/TAC.2024.3407015⟩. ⟨hal-03801100v3⟩

Y. Pechaud, N. Derlon, Isabelle Queinnec, Y. Bessiere, E. Paul. Modelling biofilm development: the importance of considering the link between EPS distribution, detachment mechanisms and physical properties. Water Research, 2024, 250, pp.120985. ⟨10.1016/j.watres.2023.120985⟩. ⟨hal-04334703⟩

Santiago Pantano Calderón, Sophie Tarbouriech, Luca Zaccarian. Plant-Order Saturated Output-Feedback Regional Controller Synthesis With Sign-Indefinite Quadratic Forms. IEEE Control Systems Letters, 2024, 8, pp.562-567. ⟨10.1109/LCSYS.2024.3397693⟩. ⟨hal-04652436⟩

Arthur Scolari Fagundes, João Manoel Gomes da Silva, Sophie Tarbouriech. A hybrid approach to the stability analysis of sampled-data Lur’e systems. Systems and Control Letters, 2024, 184, pp.105710. ⟨10.1016/j.sysconle.2023.105710⟩. ⟨hal-04866566⟩

Louis Rivière, Christian Artigues, Hélène Fargier. Two-stage stochastic/robust scheduling based on permutable operation groups. Annals of Operations Research, 2024, 332 (1-3), pp.645-687. ⟨10.1007/s10479-023-05639-1⟩. ⟨hal-04229958⟩

Alexandre Heintzmann, Christian Artigues, Pascale Bendotti, Sandra Ulrich Ngueveu, Cécile Rottner. A comparison of alternative models for solving a non-linear single plant Hydro Unit Commitment problem. Computers and Operations Research, 2024, 165, pp.106591. ⟨10.1016/j.cor.2024.106591⟩. ⟨hal-04729559⟩

Christian Artigues, Emmanuel Hébrard, Alain Quilliot, Hélène Toussaint. The Continuous Time-Resource Trade-off Scheduling Problem with Time Windows. INFORMS Journal on Computing, 2024, 36 (6), pp.1359-1756. ⟨10.1287/ijoc.2022.0142⟩. ⟨hal-04610399⟩

François Lamothe, Claudio Contardo, Matthieu Gruson. Tilted inequalities and facets of the set covering polytope: A theoretical analysis. Discrete Applied Mathematics, 2024, 357, pp.143-160. ⟨10.1016/j.dam.2024.06.004⟩. ⟨hal-04874698⟩

Zhijian Hu, Kun Zhang, Rong Su, Ruiping Wang. Robust Cooperative Load Frequency Control for Enhancing Wind Energy Integration in Multi-Area Power Systems. IEEE Transactions on Automation Science and Engineering, In press, pp.1 - 11. ⟨10.1109/tase.2024.3367030⟩. ⟨hal-04636495⟩

Kévin Ducharlet, Louise Travé-Massuyès, Jean-Bernard Lasserre, Marie-Véronique Le Lann, Youssef Miloudi. Leveraging the Christoffel function for outlier detection in data streams. International Journal of Data Science and Analytics, In press, pp.doi.org/10.1007/s41060-024-00581-2. ⟨10.1007/s41060-024-00581-2⟩. ⟨hal-04630422⟩

Felix Agner, Jonas Hansson, Pauline Kergus, Anders Rantzer, Sophie Tarbouriech, et al.. Decentralized PI-control and Anti-windup in Resource Sharing Networks. European Journal of Control, 2024, pp.101049. ⟨10.1016/j.ejcon.2024.101049⟩. ⟨hal-04270492⟩

Jean-Bernard Lasserre. The Christoffel function: Applications, connections and extensions. Numerical Algebra, Control and Optimization, In press, ⟨10.3934/naco.2024011⟩. ⟨hal-04488686⟩

Quoc Hung Lu, Soheib Fergani, Carine Jauberthie. Analytical Bounds for an Interval Kalman Filter. IEEE Transactions on Automatic Control, 2024, 69 (1), pp.449 - 454. ⟨10.1109/TAC.2023.3268307⟩. ⟨hal-04070189⟩

Loïc Michel, Caroline Braud, Jean-Pierre Barbot, Franck Plestan, Dimitri Peaucelle, et al.. Some comments on experimental results of three lift controllers for a wind turbine blade section using an active flow control. Wind Energy Science, In press, ⟨10.5194/wes-2024-15⟩. ⟨hal-04457382⟩

Jean-François Aujol, Luca Calatroni, Charles Dossal, Hippolyte Labarrière, Aude Rondepierre. Parameter-Free FISTA by Adaptive Restart and Backtracking. SIAM Journal on Optimization, 2024, 34 (4), pp.3259-3285. ⟨10.1137/23M158961X⟩. ⟨hal-04172497⟩

Ibis Velasquez, Yannick Pencolé, Euriell Le Corronc. Analysis and control of timed event graphs in (max,+) algebra for the active localization of time failures. Discrete Event Dynamic Systems, 2024, 34 (1), pp.53-93. ⟨10.1007/s10626-023-00391-x⟩. ⟨hal-04483570⟩

Jean-Bernard Lasserre. CHEBYSHEV AND EQUILIBRIUM MEASURE VS BERNSTEIN AND LEBESGUE MEASURE. Proceedings of the American Mathematical Society, In press, ⟨10.1090/proc/16739⟩. ⟨hal-04043186⟩

Simone Mariano, Riccardo Bertollo, Romain Postoyan, Luca Zaccarian. Hybrid coupling rules for leaderless heterogeneous oscillators: Uniform global asymptotic and finite-time synchronization. Automatica, 2024, 159, pp.111324. ⟨10.1016/j.automatica.2023.111324⟩. ⟨hal-04253604⟩

Vít Cibulka, Milan Korda, Tomas Hanis. Towards optimal spatio‐temporal decomposition of control‐related sum‐of‐squares programs. International Journal of Robust and Nonlinear Control, 2024, 34 (18), pp.11847-11867. ⟨10.1002/rnc.7596⟩. ⟨hal-04737856⟩

Le Toan Duong, Audine Subias, Louise Travé-Massuyès, Christophe Merle. Big data analytics for quality variation over work shifts in manufacturing systems. International Journal of Computer Integrated Manufacturing, In press, ⟨10.1080/0951192X.2024.2351529⟩. ⟨hal-04619714⟩

Andrea Mattioni, Christophe Prieur, Sophie Tarbouriech. Control design for beam stabilization with self-sensing piezoelectric actuators: managing presence and absence of hysteresis. Mathematics of Control, Signals, and Systems, 2024, 36, pp.979-1008. ⟨10.1007/s00498-024-00393-6⟩. ⟨hal-04659186⟩

Books

Nathanaël Fijalkow (Dir.). Games on Graphs. pp.1-491, In press, ⟨10.48550/arXiv.2305.10546⟩. ⟨hal-04273394⟩

Vincent Mahout, Thierry Rocacher, Guillaume Auriol. Programmation des systèmes embarqués. ISTE Group, 312 p., 2024, 9781836120049. ⟨hal-04717102⟩

Romain Postoyan, Paolo Frasca, Elena Panteley, Luca Zaccarian. Hybrid and networked dynamical systems. Springer Nature Switzerland, 493, pp.XVII, 328, 2024, Lecture Notes in Control and Information Sciences, 978-3-031-49554-0. ⟨10.1007/978-3-031-49555-7⟩. ⟨hal-04628500⟩

Book sections

Thiago Alves Lima, Sophie Tarbouriech. Dynamic allocation function design in the presence of magnitude saturating inputs. Proceedings of 2022 AWM Research Symposium, In press. ⟨hal-04643120⟩

Sophie Tarbouriech, Christophe Prieur, Isabelle Queinnec, Luca Zaccarian, Germain Garcia. Control of Uncertain Nonlinear Fully Linearizable Systems. Postoyan, R., Frasca, P., Panteley, E., Zaccarian, L. (eds). Hybrid and Networked Dynamical Systems, 493, Springer Nature Switzerland, pp.179-197, 2024, Lecture Notes in Control and Information Sciences, Print ISBN978-3-031-49554-0 ; Online ISBN978-3-031-49555-7. ⟨10.1007/978-3-031-49555-7_8⟩. ⟨hal-04776124⟩

Sophie Tarbouriech, Carla de Souza, Antoine Girard. Layers Update of Neural Network Control via Event-Triggering Mechanism. Hybrid and Networked Dynamical Systems, 493, Springer Nature Switzerland, pp.253-272, 2024, Lecture Notes in Control and Information Sciences, 978-3-031-49555-7. ⟨10.1007/978-3-031-49555-7_11⟩. ⟨hal-04527093⟩

Conference papers

Charles-Maxime Gauriat, Yannick Pencolé, Pauline Ribot, Gregory Brouillet. Multi-class Neural Additive Models : An Interpretable Supervised Learning Method for Gearbox Degradation Detection. 2024 IEEE International Conference on Prognostics and Health Management, Jun 2024, Spokane WA, United States. ⟨10.1109/ICPHM61352.2024.10627522⟩. ⟨hal-04562531⟩

Victor Magron. Trace polynomial optimization with applications in quantum information. Workshop on Semidefinite and Polynomial Optimization, Aug 2024, Amsterdam (Hollande), Netherlands. ⟨hal-04719307⟩

Ibis Velasquez, Euriell Le Corronc, Euriell Le Corronc, Yannick Pencolé. Learning normal and delayed behavior of max-plus linear systems from input and output event data. 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Aug 2024, Bari, Italy. ⟨hal-04718040⟩

Charles-Maxime Gauriat, Yannick Pencolé, Pauline Ribot, Gregory Brouillet. On a Method to Measure Supervised Multiclass Model’s Interpretability: Application to Degradation Diagnosis (Short Paper). 35th International Conference on Principles of Diagnosis and Resilient Systems (DX 2024), Nov 2024, Vienna, Austria. ⟨10.4230/OASIcs.DX.2024.27⟩. ⟨hal-04862630⟩

Quoc Hung Lu, Soheib Fergani, Carine Jauberthie. Generic Interval Filter for continuous time nonlinear systems with bounded state condition. The 63rd IEEE Conference on Decision and Control CDC'24, IEEE, Dec 2024, Milan (Italie), Italy. ⟨hal-04845940⟩

Rahma Bengamra, Soheib Fergani, Carine Jauberthie. Hyperplanes Based Zonotopic Contractor. 35th International Conference on Principles of Diagnosis and Resilient Systems (DX 2024), Nov 2024, Vienne (AUT), Austria. pp.26: 1-26: 13, ⟨10.4230/OASIcs.DX.2024.26⟩. ⟨hal-04845988⟩

Denis Arzelier, Florent Bréhard, Mioara Joldes, Marc Mezzarobba. Rounding Error Analysis of an Orbital Collision Probability Evaluation Algorithm. 31st IEEE International Symposium on Computer Arithmetic, Jun 2024, Malaga, Spain. pp.96-103, ⟨10.1109/ARITH61463.2024.00025⟩. ⟨hal-04466875⟩

Samuele Zoboli, Andreu Cecilia. k-contraction analysis for discrete-time systems. 4th IFAC Conference of Modelling, Identification and Control of Nonlinear Systems, Sep 2024, Lyon (FR), France. ⟨10.13039/501100011033⟩. ⟨hal-04643933⟩

Thalita Nazaré, Isabelle Queinnec, Erivelton Nepomuceno. Exploring Control Co-Design's Versatility in System Optimisation: A Case Study of DC Motors. 32nd Mediterranean Conference on Control and Automation (MED 2024), IEEE, Jun 2024, Chania, Crete, Greece. ⟨10.1109/MED61351.2024.10566157⟩. ⟨hal-04654734⟩

Adrien Callico, Pierre Desport, Caroline Prodhon, Jean-Charles Billaut. Optimization in short local supply chains. JIRC 2024, fédération ICVL, Nov 2024, Bourges, France. ⟨hal-04826232⟩

Santiago Pantano-Calderón, Sophie Tarbouriech, Luca Zaccarian. Global Exponential Saturated Output Feedback Design With Sign-Indefinite Quadratic Forms. European Control Conference (ECC 2024), Jun 2024, Stockholm, Sweden. pp.980-985, ⟨10.23919/ECC64448.2024.10591218⟩. ⟨hal-04672584⟩

Victor Magron. State polynomial optimization for nonlinear Bell inequalities. Effective Methods in Algebraic Geometry, Jul 2024, Leipzig, Germany. ⟨hal-04719283⟩

Florian Sansou, Gautier Hattenberger, Luca Zaccarian, Fabrice Demourant, Thomas Loquen. Modelling and Hovering Stabilisation of a Free-Rotating Wing UAV. 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Jun 2024, La Canée (Crete), Greece. pp.779-785, ⟨10.1109/ICUAS60882.2024.10556832⟩. ⟨hal-04619809⟩

Aneel Tanwani, Olga Yufereva. Convergence Analysis of Ensemble Filters for Linear Stochastic Systems with Poisson-Sampled Observations. International Symposium on Mathematical Theory of Networks and Systems, Aug 2024, Cambridge, United Kingdom. ⟨hal-04616321⟩

Patricia Monica Campos-Mayer-Vicente, Felipe Gomes Cabral, Públio M. Lima, Marcos Vicente Moreira, Audine Subias, et al.. Transparência Baseada em Propriedade: uma Nova Noção de Utilidade para Sistemas a Eventos Discretos ⋆. XXV Congresso Brasileiro de Automática, Oct 2024, Rio de Janeiro (BR), Brazil. ⟨hal-04775872⟩

Patricia Monica Campos-Mayer-Vicente, Felipe Gomes Cabral, Públio M. Lima, Marcos Vicente Moreira, Audine Subias, et al.. Property-Based Transparency: a New Utility Definition*. 2024 IEEE 20th International Conference on Automation Science and Engineering, Aug 2024, Bari (IT), Italy. ⟨hal-04775876⟩

Florian Bethencourt, Hélène Blasco, Marina Vinot, Jean-Charles Billaut. Optimisation des déplacements d'échantillons médicaux. 25ème congrès annuel de la Société Française de Recherche Opérationnelle et d'Aide à la Décision (ROADEF 2024), Mar 2024, Amiens, France. ⟨hal-04623403⟩

Manon Doré, Yassine Ariba, Oswaldo Lopez-Santos, Germain Garcia. Revisiting the argmin direct control for the Cascaded H-Bridge Inverter. Conference on Control Technology and Applications CCTA 2024, Aug 2024, Newcastel upon Tyne, United Kingdom. ⟨10.1109/CCTA60707.2024.10666589⟩. ⟨hal-04627060v2⟩

Maxence Glotin, Louise Travé-Massuyès, Elodie Chanthery. MSO sets and MTES for dummies. The 35th International Conference on Principles of Diagnosis and Resilient Systems (DX'24), Nov 2024, Vienna (Autriche), Austria. ⟨10.4230/OASIcs.DX.2024.13⟩. ⟨hal-04777448⟩

Silke Merkelbach, Alexander Diedrich, Anna Sztyber-Betley, Louise Travé-Massuyès, Elodie Chanthery, et al.. Using Multi-modal LLMs to Create Models for Fault Diagnosis. The 35th International Conference on Principles of Diagnosis and Resilient Systems (DX'24), Nov 2024, Vienna, Austria. ⟨10.4230/OASIcs.DX.2024.6⟩. ⟨hal-04777473⟩

A Callico, P Desport, C Prodhon, Jean-Charles Billaut. Sharing deliveries in a short food logistic context. 33rd European Conference on Operational Research, Jun 2024, Copenhagen, Denmark. ⟨hal-04623649⟩

Jean-Charles Billaut, H Blasco, Marina Vinot. Dispatching medical samples: a case study. 33rd European Conference on Operational Research, Jun 2024, Copenhague, Denmark. ⟨hal-04623657⟩

Elouan Blanchard, Arthur Bit-Monnot, Cyrille Briand, Grégoire Milliez, Mohamed Amine Abdeljaouad. Planning the tasks of an autonomous mobile robot fleet for internal logistics of production systems. APMS 2024 CONFERENCE, Sep 2024, Chemnitz/Zwickau, Germany. ⟨hal-04642887⟩

Carla Juvin, Laurent Houssin, Pierre Lopez. Two-stage approaches to solving the robust job-shop problem with uncertainty budget. 19th International Workshop on Project Management and Scheduling (PMS 2024), Apr 2024, Bern, Switzerland. ⟨hal-04675753⟩

Adrien Callico, Jean-Charles Billaut, Pierre Desport, Caroline Prodhon. Optimisation dans les circuits courts de proximité. 25ème congrès annuel de la Société Française de Recherche Opérationnelle et d'Aide à la Décision (ROADEF 2024), Société Française de Recherche Opérationnelle et d'Aide à la Décision, Mar 2024, Amiens, France. ⟨hal-04510028⟩

Yoshio Ebihara, Xin Dai, Victor Magron, Dimitri Peaucelle, Sophie Tarbouriech. Local Lipschitz Constant Computation of ReLU-FNNs: Upper Bound Computation with Exactness Verification. European Control Conference (ECC 2024), Jun 2024, Stockholm, Sweden. ⟨10.23919/ECC64448.2024.10590974⟩. ⟨hal-04247204⟩

Aneel Tanwani. On Analyzing Filters with Bayesian Parameter Inference and Poisson-Sampled Observations. IEEE Conference on Decision and Control, Dec 2024, Milan (Italie), Italy. ⟨hal-04855941⟩

Valentin Antuori, Damien T Wojtowicz, Emmanuel Hebrard. A Stable-Set-Based Move to Solve an Agile Earth Observation Satellite Scheduling Problem with a Local Search. 25ème congrès annuel de la Société française de recherche opérationnelle et d'aide à la décision (ROADEF 2024), Mar 2024, Amiens, France. https://roadef2024.sciencesconf.org/511480. ⟨hal-04519736⟩

Camille Lescuyer, Christian Artigues, Jean-Thomas Camino, Cédric Pralet. Heuristic Methods for the Antenna-Constrained Beam Layout Optimization on Multibeam Broadcasting Mission. 13th International Conference on Operations Research and Enterprise Systems, Feb 2024, Rome, Italy. pp.294-301, ⟨10.5220/0012380200003639⟩. ⟨hal-04521756⟩

Mattia Giaccagli, Marc Jungers, Sophie Tarbouriech. Some LMIs for the design of dynamic output feedback contractive controllers for a class of nonlinear systems. 4th IFAC Conference of Modelling, Identification and Control of Nonlinear Systems, MICNON 2024, Sep 2024, Lyon, France. ⟨10.1016/j.ifacol.2024.10.145⟩. ⟨hal-04692897⟩

Guillaume Poujade, Jean-Charles Billaut, Denis Martouzet, Jean-François Raze. Interdiction problems and innovation networks. 25ème congrès annuel de la Société Française de Recherche Opérationnelle et d'Aide à la Décision (ROADEF 2024), Mar 2024, Amiens, France. ⟨hal-04623589⟩

Mallory Taffonneau, Jean-Charles Billaut, Ronan Bocquillon. Caractérisation des solutions optimales du 1||Lmax. 25ème congrès annuel de la Société Française de Recherche Opérationnelle et d'Aide à la Décision (ROADEF 2024), Mar 2024, Amiens, France. ⟨hal-04623626⟩

Alexandre Seuret, Rafael Vazquez, Luca Zaccarian. A Hybrid Dynamical System Approach to the Impulsive Control of Spacecraft Rendezvous. 2024 European Control Conference (ECC), Jun 2024, Stockholm, Sweden. pp.1479-1484, ⟨10.23919/ECC64448.2024.10590979⟩. ⟨hal-04676163⟩

Swantje Plambeck, Maximilian Schmidt, Goerschwin Fey, Audine Subias, Louise Travé-Massuyès. Dynamics-Based Identification of Hybrid Systems using Symbolic Regression. DSD/SEAA Conference, Aug 2024, Paris, France. ⟨hal-04794430⟩

Louis Goupil, Louise Travé-Massuyès, Elodie Chanthery, Thibault Kohler, Sébastien Delautier. Tree based Diagnosis Enhanced with Meta Knowledge Applied to Dynamic Systems. 12th IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes (2024), Best Theory Paul M. Frank paper Award, IFAC, Jun 2024, Ferrara, Italy. to appear in IFAC-PapersOnLine. ⟨hal-04556203⟩

Swantje Plambeck, Maximilian Schmidt, Audine Subias, Louise Travé-Massuyès, Goerschwin Fey. Usability of Symbolic Regression for Hybrid System Identification -System Classes and Parameters. The 35th International Conference on Principles of Diagnosis and Resilient Systems (DX'24), Nov 2024, Vienna, Austria. 14 p., ⟨10.4230/OASIcs.DX.2024.30⟩. ⟨hal-04794459⟩

Louise Travé-Massuyès, Kévin Ducharlet, Jean-Bernard Lasserre. Leveraging the properties of the Christoffel function for anomaly detection in data streams. Congrès Annuel de la SAGIP, SAGIP, May 2024, Lyon, France. ⟨hal-04794461⟩

Saroj Prasad Chhatoi, Aneel Tanwani, Didier Henrion. Optimal Control of Nonsmooth Dynamical Systems using Measure Relaxations. IEEE Conference on Decision and Control, IEEE, Dec 2024, Milan (Italie), Italy. ⟨hal-04701838⟩

Tanguy Terrien, Cyrille Briand, Philippe Truillet. A CP model with aggregation for real-life project scheduling. 25ème Congrès annuel de la Société Française de Recherche Opérationnelle et d'Aide à la Décision (ROADEF 2024), Mar 2024, Amiens, France. à paraître. ⟨hal-04353470⟩

Yukai Tang, Jean-Bernard Lasserre, Heng Yang. Uncertainty Quantification of Set-Membership Estimation in Control and Perception: Revisiting the Minimum Enclosing Ellipsoid. L4DC 2024, Jul 2024, Oxford (UK), France. pp.1--36. ⟨hal-04697144⟩

Karim Terfasse, Ghassen Cherif, Marie-José Huguet. Integer Linear Programming for Automated Guided Vehicles Path Planning in Container Terminals. International Conférence on Control, Decision and Information Technologies (CoDIT 2024), Jul 2024, Valleta, Malta. ⟨hal-04704943⟩

Julien Ferry, Ulrich Aïvodji, Sébastien Gambs, Marie-José Huguet, Mohamed Siala. Probabilistic Dataset Reconstruction from Interpretable Models. 2nd IEEE Conference on Secure and Trustworthy Machine Learning, Apr 2024, Toronto, Canada. ⟨10.1109/SaTML59370.2024.00009⟩. ⟨hal-04189566v2⟩

Manon Doré, Nicola Zaupa. Control of the RMS Output Current in Series Resonant Converters. 4th IFAC Conference of Modelling, Identification and Control of nonlinear systems (MICNON 2024), Sep 2024, Lyon, France. pp.132-137, ⟨10.1016/j.ifacol.2024.10.159⟩. ⟨hal-04627710v2⟩

Dimitri Peaucelle, Yoshio Ebihara, Yohei Hosoe. About an alternative S-variable condition for state-feedback design. European Control Conference, EUCA, Jun 2024, Stockholm, Sweden. ⟨10.23919/ECC64448.2024.10591320⟩. ⟨hal-04266433⟩

Matthieu Masson, Christian Artigues, Denis Arzelier, Fabrizio Dabbene, Mioara Joldeş, et al.. Impulsive thrust collision avoidance for long-term space encounters. 63rd IEEE Conference on Decision and Control, Dec 2024, Milan (Italie), Italy. ⟨hal-04710416⟩

Léonie Hatte, Pauline Ribot, Elodie Chanthery. Transforming Time Petri Nets into Heterogeneous Petri Nets for Hybrid System Monitoring. IFAC Safeprocess 2024, Jun 2024, Ferrara, Italy. ⟨hal-04578700⟩

Bruno Loff, Mateusz Skomra. Smoothed Analysis of Deterministic Discounted and Mean-Payoff Games. 51st International Colloquium on Automata, Languages, and Programming (ICALP 2024), Jul 2024, Tallinn, Estonia. pp.147:1-147:16, ⟨10.4230/LIPIcs.ICALP.2024.147⟩. ⟨hal-04762619⟩

Nicola Zaupa, Luca Zaccarian, Sophie Tarbouriech, Isabelle Queinnec, Giulia Giordano. Controlling identical linear multi-agent systems over directed graphs. 2023 IEEE 62st Conference on Decision and Control (CDC), IEEE, Dec 2023, Singapore, Singapore. pp.7395-7400, ⟨10.1109/CDC49753.2023.10383830⟩. ⟨hal-04357943⟩

Patrícia C Mayer, Felipe G Cabral, Públio M M Lima, Marcos V Moreira, Audine Subias, et al.. Property-Based Transparency: a New Utility Definition. International Conference on Automation Science and Engineering, Aug 2024, Bari, Italy. ⟨hal-04795602⟩

Julien Rouzot, Joséphine Gobert, Christian Artigues, Romain Boyer, Frédéric Camps, et al.. Scheduling onboard tasks of the NIMPH nanosatellite. 13th International Conference on Operations Research and Enterprise Systems (ICORES), Feb 2024, Rome, Italy. ⟨hal-04430171⟩

Other documents

Manon Doré, Yassine Ariba, Germain Garcia. The power balance equation for converter control - Application to a three-level neutral point clamped rectifier. Methods and Algorithms for the Control of Complex Systems, Aug 2024, Banyuls-sur-mer, France. ⟨hal-04735611⟩

Nicola Zaupa, Giulia Giordano, Isabelle Queinnec, Sophie Tarbouriech, Luca Zaccarian. Equivalent Conditions for the Synchronization of Identical Linear Systems. Workshop "Methods and Algorithms for the Control of Complex Systems", Aug 2024, Banyuls sur-mer, France, France. 2024. ⟨hal-04700228⟩

Srećko Đurašinović, Jianting Yang, Jean-Bernard Lasserre, Victor Magron, Jun Zhao. Verifying Properties of Binary Neural Networks Using Sparse Polynomial Optimization. R&T Days 2024, Jul 2024, Toulouse (FRANCE), France. 2024. ⟨hal-04720757⟩

Santiago Pantano Calderón, Sophie Tarbouriech, Luca Zaccarian. Output-feedback controller synthesis with sign-indefinite quadratic forms. Workshop Methods and Algorithms for the Control of Complex Systems, Aug 2024, Banyuls-sur-Mer, France. ⟨hal-04698747⟩

Sara Callegari, Frédéric Gouaisbaut, Dimitri Peaucelle. Robustness of Coupled ODEs and PDEs, state-of-the-art and perspectives. Methods and Algorithms for the Control of Complex Systems, Aug 2024, Banyuls sur-mer, France, France. 2024. ⟨hal-04700288⟩

Nicola Zaupa, Carlos Olalla, Isabelle Queinnec, Luis Martínez-Salamero, Luca Zaccarian. Hybrid Control of Resonant Converters. Workshop "Methods and Algorithms for the Control of Complex Systems", Aug 2024, Banyuls sur-mer, France, France. 2024. ⟨hal-04700237⟩

Saroj Prasad Chhatoi. Optimal Control of a Nonsmooth Dynamical System using Measure Relaxation. Methods and Algorithms for the Control of Complex Systems, Aug 2024, Banyuls - sur - Mer, France. 2024. ⟨hal-04698728⟩

Tanguy Terrien, Philippe Truillet, Cyrille Briand. Human-centered decision-aid for dynamic activity planning in production systems. RJC IHM 2024, Sep 2024, Oléron, France. ⟨hal-04739745⟩

D Lacal Ip, Y Bourlier, G Delport, Vincent Boitier, Vincent Mahout, et al.. CABLE SOLAR: Small Unit Aerostat for Solar Generation. IPVF Days, May 2024, Palaiseau (91), France. 2024. ⟨hal-04730979⟩

Charles-Maxime Gauriat, Yannick Pencolé, Pauline Ribot, Gregory Brouillet. Modèles Additifs Neuronaux Multi classes (MNAM). LAAS Research and Technology Days 2024 (RTDAYS), Jul 2024, Toulouse, France. 2024. ⟨hal-04775898⟩

Proceedings

Yukai Tang, Jean-Bernard Lasserre, Heng Yang. Uncertainty Quantification of Set-Membership Estimation in Control and Perception: Revisiting the Minimum Enclosing Ellipsoid. L4DC 2024, Proceedings of Machine Learning Research, 242, PMLR, pp.286--298, 2024. ⟨hal-04311534⟩

Shingo Nishinaka, Rin Saeki, Tsuyoshi Yuno, Yoshio Ebihara, Victor Magron, et al.. Stability Analysis of Feedback Systems with ReLU Nonlinearities via Semialgebraic Set Representation. 4th IFAC Conference of Modelling, Identification and Control of nonlinear systems (MICNON), 2024. ⟨hal-04495314⟩

Lucas Lima Lopes, Louise Travé-Massuyès, Carine Jauberthie, Guillaume Alcalay. A Review of Fault Diagnosis Techniques Applied to Aircraft Air Data Sensors. International Conference on Principles of Diagnosis and Resilient Systems (DX), Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2024, 978-3-95977-356-0. ⟨10.4230/OASIcs.DX.2024.3⟩. ⟨hal-04849194⟩

Igor Klep, Victor Magron, Gaël Massé, Jurij Volčič. Upper bound hierarchies for noncommutative polynomial optimization. 26th International Symposium on Mathematical Theory of Networks and Systems (MTNS), 2024. ⟨hal-04440949⟩

@softwareversion

Yannick Pencolé. DdAutomata (Automata tools). 2024, ⟨swh:1:dir:66a436ed79218d8109f9927cd1281e3bf431274a;origin=https://gitlab.laas.fr/ypencole/ddautomata;visit=swh:1:snp:5c1726eef243ee48acf81a695b3db87a84e29165;anchor=swh:1:rev:6cf0cd89ea8e6d030258d48895eb7ce6daf8456f⟩. ⟨hal-04779083⟩

Victor Magron, Jie Wang. TSSOS. 2024, ⟨swh:1:dir:cbf2ecc0d62a29200571c1fefaab9e97d62fb6a4;origin=https://hal.archives-ouvertes.fr/hal-04719510;visit=swh:1:snp:99ab25528c5694b6e3de07baa33fab62d9ba3b25;anchor=swh:1:rel:7933a8a0093f3fae2d54c3bb5c3edd84b6ed16b5;path=/⟩. ⟨hal-04719510⟩

Yannick Pencolé. DdPetri (Petri net collection tools of Diades). 2024, ⟨swh:1:dir:ecce6e0ecc61d35a6e903d0745f40315e7739daa;origin=https://gitlab.laas.fr/ypencole/ddpetri;visit=swh:1:snp:97bceb647ac1d1e940e1bea79828d1d91c2ba6d1;anchor=swh:1:rev:06bfdca77a59b680a0eaa9769bc1017df19041b0⟩. ⟨hal-04779090⟩

Victor Magron. RealCertify. 2024, ⟨swh:1:dir:65138ea897686eed5531074255caa4dd21d087b4;origin=https://hal.archives-ouvertes.fr/hal-04719526;visit=swh:1:snp:e32a3b48f1744a2714f5f9ddbf411cc278807f96;anchor=swh:1:rel:c474cafbf7034e92b0fe2e165b1355af844bf4c2;path=/⟩. ⟨hal-04719526⟩

Yannick Pencolé. diades (DIAgnosis of Discrete Event Systems). 2024, ⟨swh:1:dir:f0c1d9fdd38a0ee1f8d37eb408428c4d603ddf2c;origin=https://gitlab.laas.fr/ypencole/diades;visit=swh:1:snp:e9d3cccd3c6b0feea44623139cca7b121a0fb1d4;anchor=swh:1:rev:d983dfe2ee50b18f9f22cdc1e7b1b669ead46844⟩. ⟨hal-04779011⟩

Yannick Pencolé. DdEditor (Diades editor). 2024, ⟨swh:1:dir:3752fea19639a763fe00156c1d557be6fc520f51;origin=https://gitlab.laas.fr/ypencole/ddeditor;visit=swh:1:snp:f078c4952f459c8a32061c2578eb38812ad62a65;anchor=swh:1:rev:7a7501caa360322a91dae69cf33439ea51db4d7f⟩. ⟨hal-04779018⟩

Preprints, Working Papers, ...

Mareike Dressler, Simon Foucart, Mioara Joldeş, Etienne de Klerk, Jean-Bernard Lasserre, et al.. Least multivariate Chebyshev polynomials on diagonally determined domains. 2024. ⟨hal-04727563⟩

Aloïs Duguet, Margarida Carvalho, Gabriele Dragotto, Sandra Ulrich Ngueveu. Computing Approximate Nash Equilibria for Integer Programming Games. 2024. ⟨hal-04449901⟩

Andreu Cecilia, Samuele Zoboli, Daniele Astolfi, Ulysse Serres, Vincent Andrieu. Generalized Lyapunov conditions for k-contraction: analysis and feedback design. 2024. ⟨hal-04300588v2⟩

Alexandre Heintzmann, Pascale Bendotti, Cécile Rottner. Handling polyhedral symmetries with a dedicated Branch&Cut: application to a knapsack variant. 2024. ⟨hal-04493165v2⟩

Anubhab Dasgupta, Aneel Tanwani. Steady State and Fluctuation Analysis for Kalman Filters with Poisson-Sampled Observations. 2024. ⟨hal-04798886⟩

Didier Henrion, Jean Bernard Lasserre. Approximate D-optimal design and equilibrium measure *. 2024. ⟨hal-04688534⟩

Didier Henrion. Infinite-dimensional Christoffel-Darboux polynomial kernels on Hilbert spaces. 2024. ⟨hal-04628265⟩

Didier Henrion, Jean-Bernard Lasserre. An infinite-dimensional Christoffel function and detection of abnormal trajectories. 2023. ⟨hal-04631100⟩

Timothée Ly, Julien Ferry, Marie-José Huguet, Sébastien Gambs, Ulrich Aivodji. Smooth Sensitivity for Learning Differentially-Private yet Accurate Rule Lists. 2024. ⟨hal-04505410v2⟩

Didier Henrion, Adrien Le Franc, Victor Magron. Slow convergence of the moment-SOS hierarchy for an elementary polynomial optimization problem. 2024. ⟨hal-04500960v4⟩

Felix Huber, Victor Magron, Jurij Volčič. Positivity of state, trace, and moment polynomials, and applications in quantum information. 2024. ⟨hal-04844939⟩

Jean-François Aujol, Charles Dossal, Hippolyte Labarrière, Aude Rondepierre. Strong Convergence of FISTA Iterates under Hölderian and Quadratic Growth Conditions. 2024. ⟨hal-04660448⟩

Rafael Accácio Nogueira, Soheib Fergani, Jan Bolting. Constrained Zonotope-based localization of mobile agents with uncertain observation times. 2024. ⟨hal-04845892⟩

Agustín G Yabo, Nicolas Augier. On L¹ and time-optimal state transitions in piecewise linear models of gene-regulatory networks. 2024. ⟨hal-04820387⟩

Didier Henrion, Mauricio Junca, Mauricio Velasco. Moment-SOS hierarchy and exit location of stochastic processes. 2024. ⟨hal-03110452v3⟩

Benoît Bonnet-Weill, Milan Korda. Set-Valued Koopman Theory for Control Systems. 2024. ⟨hal-04408228⟩

Jianting Yang, Srećko Ðurašinović, Jean-Bernard Lasserre, Victor Magron, Jun Zhao. Verifying Properties of Binary Neural Networks Using Sparse Polynomial Optimization. 2024. ⟨hal-04589986⟩

Denis Arzelier, Florent Bréhard, Tom Hubrecht, Mioara Joldes. An Exchange Algorithm for Optimizing both Approximation and Finite-Precision Evaluation Errors in Polynomial Approximations. 2024. ⟨hal-04709615⟩

Denis Arzelier, Mioara Joldeş, Matthieu Masson. Efficient Evaluation of 2-D Collision Probability Derivatives for Uncertain k-scaled Covariances: A PcMax Case Study. 2024. ⟨hal-04710373⟩

Didier Henrion, Alessandro Rudi. Solving moment and polynomial optimization problems on Sobolev spaces. 2024. ⟨hal-04393205v2⟩

Jean-Bernard Lasserre. A hierarchy of convex relaxations for the total variation distance. 2024. ⟨hal-04367575v3⟩

Florian Sansou, Fabrice Demourant, Gautier Hattenberger, Thomas Loquen, Luca Zaccarian. Hovering stabilization of the DarkO tail-sitter drone with constant wind. 2024. ⟨hal-04715046⟩

Julien Ferry, Ulrich Aïvodji, Sébastien Gambs, Marie-José Huguet, Mohamed Siala. Taming the Triangle: On the Interplays between Fairness, Interpretability and Privacy in Machine Learning. 2024. ⟨hal-04359832v2⟩

Enky Oudot, Gaël Massé, Xavier Valcarce, Antonio Acín. Realistic Bell tests with homodyne measurements. 2024. ⟨hal-04470732⟩

Charlotte Lacoquelle, Xavier Pucel, Louise Travé-Massuyès, Axel Reymonet, Benoît Enaux. Warped Time Series Anomaly Detection. 2024. ⟨hal-04549643⟩

Samuele Zoboli, Andreu Cecilia, Sophie Tarbouriech. Quadratic abstractions for k-contraction. 2024. ⟨hal-04619425⟩

Jared Miller, Matteo Tacchi, Didier Henrion, Mario Sznaier. Unsafe Probabilities and Risk Contours for Stochastic Processes using Convex Optimization. 2023. ⟨hal-04382156⟩

Saroj Prasad Chhatoi, Didier Henrion, Swann Marx, Nicolas Seguin. Optimizing quasi-dissipative evolution equations with the moment-SOS hierarchy. 2024. ⟨hal-04828131⟩

Hibiki Gyotoku, Tsuyoshi Yuno, Yoshio Ebihara, Victor Magron, Dimitri Peaucelle, et al.. On Dual of LMIs for Absolute Stability Analysis of Nonlinear Feedback Systems with Static O'Shea-Zames-Falb Multipliers. 2024. ⟨hal-04797364⟩

Antonio Bellon, Didier Henrion, Vyacheslav Kungurtsev, Jakub Mareček. Parametric Semidefinite Programming: Geometry of the Trajectory of Solutions. 2024. ⟨hal-03196925v3⟩

Jean-François Aujol, Charles Dossal, Hippolyte Labarrière, Aude Rondepierre. Heavy Ball Momentum for Non-Strongly Convex Optimization. 2024. ⟨hal-04500652⟩

Yoshio Ebihara, Noboru Sebe, Hayato Waki, Dimitri Peaucelle, Sophie Tarbouriech, et al.. Induced Norm Analysis of Linear Systems for Nonnegative Input Signals. 2024. ⟨hal-04438031⟩

Saroj Prasad Chhatoi, Aneel Tanwani, Didier Henrion. Evolution of Measures in Nonsmooth Dynamical Systems: Formalisms and Computation. 2024. ⟨hal-04570185⟩

Lucie Baudouin, A Imba, A Mercado, A Osses. Lipschitz Stability of an Inverse Problem of Transmission Waves with Variable Jumps. 2024. ⟨hal-04688851⟩

Samuele Zoboli, Daniele Astolfi, Vincent Andrieu, Giacomo Casadei, Luca Zaccarian. Incremental stabilization and multi-agent synchronization of discrete-time nonlinear systems. 2024. ⟨hal-04444190v2⟩

Mareike Dressler, Simon Foucart, Mioara Joldeş, Etienne de Klerk, Jean-Bernard Lasserre, et al.. Optimization-Aided Construction of Multivariate Chebyshev Polynomials. 2024. ⟨hal-04727486⟩

Samuele Zoboli, Andreu Cecilia, Sophie Tarbouriech. Dynamic output-feedback design for generalized Lyapunov inequalities. 2024. ⟨hal-04738534⟩

2023

Journal articles

Igor Klep, Victor Magron, Jurij Volčič, Jie Wang. State polynomials: positivity, optimization and nonlinear Bell inequalities. Mathematical Programming, 2023, 207 (1-2), pp.645-691. ⟨10.1007/s10107-023-02024-5⟩. ⟨hal-03964830⟩

Victor Magron, Jie Wang. SONC Optimization and Exact Nonnegativity Certificates via Second-Order Cone Programming. Journal of Symbolic Computation, 2023, 115, pp.346-370. ⟨10.1016/j.jsc.2022.08.002⟩. ⟨hal-03070864⟩

Michael Schwegel, Tobias Glück, Vitaly Shaferman, Luca Zaccarian, Andreas Kugi. Adaptive Two-Degrees-of-Freedom Current Control for Solenoids: Theoretical Investigation and Practical Application. IEEE Transactions on Control Systems Technology, 2023, 31 (3), pp.1078-1091. ⟨10.1109/TCST.2022.3211457⟩. ⟨hal-04253602⟩

Felix Agner, Pauline Kergus, Anders Rantzer, Sophie Tarbouriech, Luca Zaccarian. Anti-windup coordination strategy around a fair equilibrium in resource sharing networks. IEEE Control Systems Letters, 2023, 7, pp.2521 - 2526. ⟨10.1109/LCSYS.2023.3287252⟩. ⟨hal-04132680⟩

Xue Han, Rim Rammal, Menglin He, Zetao Li, Michel Cabassud, et al.. Dynamic and sensor fault tolerant control for an intensified heat-exchanger/reactor. European Journal of Control, 2023, 69, pp.100736. ⟨10.1016/j.ejcon.2022.100736⟩. ⟨hal-04187728⟩

Elodie Chanthery, P-E Hladik, Corinne Joffre, G. Le Corre, J. Lesauvage, et al.. JePeIA : de la création à la mise en oeuvre d’un escape game à visée pédagogique sur l’Intelligence Artificielle. Journal sur l'enseignement des sciences et technologies de l'information et des systèmes, 2023, 22, pp.0003. ⟨10.1051/j3ea/20230003⟩. ⟨hal-04273184⟩

Filippo D’ippolito, Giovanni Garraffa, Antonino Sferlazza, Luca Zaccarian. A Hybrid Observer for Localization from Noisy Inertial Data and Sporadic Position Measurements. Nonlinear Analysis: Hybrid Systems, 2023, 49, pp.101360. ⟨10.1016/j.nahs.2023.101360⟩. ⟨hal-04253607⟩

Milan Korda, Monique Laurent, Victor Magron, Andries Steenkamp. Exploiting ideal-sparsity in the generalized moment problem with application to matrix factorization ranks. Mathematical Programming, 2023, 205, pp.703-744. ⟨10.1007/s10107-023-01993-x⟩. ⟨hal-03782934⟩

Corentin Boennec, Lucas Albuquerque, Bruno Sareni, Fabien Lacressonnière, Sandra Ulrich Ngueveu. Comparison of Battery Models Integrating Energy Efficiency and Aging for the Design of Microgrids. Smart Grids and Sustainable Energy, 2023, 9, pp.1. ⟨10.1007/s40866-023-00174-1⟩. ⟨hal-04369844⟩

Mattia Giaccagli, Vincent Andrieu, Sophie Tarbouriech, Daniele Astolfi. LMI conditions for contraction, integral action, and output feedback stabilization for a class of nonlinear systems. Automatica, 2023, 154, pp.111106. ⟨10.1016/j.automatica.2023.111106⟩. ⟨hal-04093784⟩

W P M H Heemels, Aneel Tanwani. Existence and Completeness of Solutions to Extended Projected Dynamical Systems and Sector-Bounded Projection-Based Controllers. IEEE Control Systems Letters, 2023, 7, pp.1590-1595. ⟨10.1109/LCSYS.2023.3274954⟩. ⟨hal-04161682⟩

Khazhgali Kozhasov, Jean-Bernard Lasserre. Volumes of sublevel sets of nonnegative forms and complete monotonicity. SIAM Journal on Applied Algebra and Geometry, 2023, 7 (4), ⟨10.1137/22M1502458⟩. ⟨hal-03693810⟩

Marco Bolignari, Gianluca Rizzello, Luca Zaccarian, Marco Fontana. Lightweight Human-Friendly Robotic Arm based on Transparent Hydrostatic Transmissions. IEEE Transactions on Robotics, 2023, 39 (5), pp.4051-4064. ⟨10.1109/TRO.2023.3290310⟩. ⟨hal-04253609⟩

C. de Souza, Sophie Tarbouriech, A. Girard. Event-Triggered Neural Network Control for LTI Systems. IEEE Control Systems Letters, 2023, 7, pp.1381-1386. ⟨10.1109/LCSYS.2023.3242835⟩. ⟨hal-04003097⟩

Valentina Breschi, Luca Zaccarian, Simone Formentin. Data-Driven Stabilization of Input-Saturated Systems. IEEE Control Systems Letters, 2023, 7, pp.1640-1645. ⟨10.1109/LCSYS.2023.3266254⟩. ⟨hal-04117896⟩

Jean-François Aujol, Charles Dossal, Văn Hào Hoàng, Hippolyte Labarrière, Aude Rondepierre. Fast convergence of inertial dynamics with Hessian-driven damping under geometry assumptions. Applied Mathematics and Optimization, 2023, 88 (81). ⟨hal-03693218v2⟩

Riccardo Ballaben, Uros Sutulovic, Davide Invernizzi, Luca Zaccarian. A hybrid redesign for robust stabilization without unit input. IEEE Control Systems Letters, 2023, 7, pp.2575-2580. ⟨10.1109/LCSYS.2023.3287670⟩. ⟨hal-04253611⟩

Jean-Bernard Lasserre. Pell's equation, sum-of-squares and equilibrium measures of a compact set. Comptes Rendus. Mathématique, 2023, 361 (1), pp.935-952. ⟨10.5802/crmath.465⟩. ⟨hal-03813195v2⟩

Ignacio Sanchez, Christophe Louembet, Marcelo Actis, Alejandro Gonzalez. Characterization and computation of control invariant sets for linear impulsive control systems. Nonlinear Analysis: Hybrid Systems, 2023, 47, pp.101271. ⟨10.1016/j.nahs.2022.101271⟩. ⟨hal-04818455⟩

Lucas Dal Bosco, Xavier Franceries, Blandine Romain, François Smekens, François Husson, et al.. A convolutional neural network model for EPID‐based non‐transit dosimetry. Journal of Applied Clinical Medical Physics, 2023, 24 (6), pp.13923. ⟨10.1002/acm2.13923⟩. ⟨hal-04782079⟩

Alexandre Seuret, Sophie Tarbouriech. A Data-Driven Approach to the L2 Stabilization of Linear Systems Subject to Input Saturations. IEEE Control Systems Letters, 2023, 7, pp.1646-1651. ⟨10.1109/LCSYS.2023.3267022⟩. ⟨hal-04203667⟩

Sigurdur Hafstein, Aneel Tanwani. Linear programming based lower bounds on average dwell-time via multiple Lyapunov functions. European Journal of Control, 2023, 74, pp.100838. ⟨10.1016/j.ejcon.2023.100838⟩. ⟨hal-04161620⟩

Ulrich Aïvodji, Julien Ferry, Sébastien Gambs, Marie-José Huguet, Mohamed Siala. Improving Fairness Generalization Through a Sample-Robust Optimization Method. Machine Learning, 2023, Special Issue on Safe and Fair Machine Learning, 112 (6), pp.2131-2192. ⟨10.1007/s10994-022-06191-y⟩. ⟨hal-03709547⟩

Christian Bessiere, Clement Carbonnel, Anton Dries, Emmanuel Hebrard, George Katsirelos, et al.. Learning Constraints through Partial Queries. Artificial Intelligence, 2023, 319, pp.103896. ⟨10.1016/j.artint.2023.103896⟩. ⟨lirmm-04028358⟩

Jean-Bernard Lasserre. A modified Christoffel function and its asymptotic properties. Journal of Approximation Theory, 2023, 295, pp.105955. ⟨10.1016/j.jat.2023.105955⟩. ⟨hal-03949201v2⟩

Santiago Pantano-Calderón, Sophie Tarbouriech, Luca Zaccarian. Local Static Anti-Windup Design With Sign-Indefinite Quadratic Forms. IEEE Control Systems Letters, 2023, 7, pp.3090-3095. ⟨10.1109/LCSYS.2023.3291232⟩. ⟨hal-04253603⟩

Imane Oussakel, Philippe Owezarski, Pascal Berthou, Laurent Houssin. Toward Radio Access Network Slicing Enforcement in Multi-Cell 5G System. Journal of Network and Systems Management, 2023, 31, pp.8. ⟨10.1007/s10922-022-09694-0⟩. ⟨hal-02633510v2⟩

Jie Wang, Victor Magron. A real moment-HSOS hierarchy for complex polynomial optimization with real coefficients. Computational Optimization and Applications, 2023, ⟨10.1007/s10589-024-00617-0⟩. ⟨hal-04189927⟩

Edgar Hernando Sepúlveda-Oviedo, Louise Travé-Massuyès, Audine Subias, Marko Pavlov, Corinne Alonso. Fault diagnosis of photovoltaic systems using artificial intelligence: A bibliometric approach. Heliyon, 2023, 9 (11), pp.e21491. ⟨10.1016/j.heliyon.2023.e21491⟩. ⟨hal-04276780⟩

Nicola Zaupa, Carlos Olalla, Isabelle Queinnec, Luis Martínez-Salamero, Luca Zaccarian. Hybrid Control of Self-Oscillating Resonant Converters With Three-Level Input. IEEE Control Systems Letters, 2023, 7, pp.1375-1380. ⟨10.1109/LCSYS.2023.3240887⟩. ⟨hal-03985922⟩

Christian Bessiere, Clément Carbonnel, Martin Cooper, Emmanuel Hebrard. Complexity of minimum-size arc-inconsistency explanations. Constraints, 2023, 28, pp.427-449. ⟨10.1007/s10601-023-09360-5⟩. ⟨hal-04275512⟩

Suha Shreim, Francesco Ferrante, Christophe Prieur. Anti-Windup Design for a Reaction-Diffusion Equation. IEEE Control Systems Letters, 2023, 7, pp.3120-3125. ⟨10.1109/LCSYS.2023.3292048⟩. ⟨hal-04132967⟩

Carla Juvin, Laurent Houssin, Pierre Lopez. Logic-based Benders decomposition for the preemptive Flexible Job-Shop Scheduling Problem. Computers & Operations Research, 2023, 152, ⟨10.1016/j.cor.2023.106156⟩. ⟨hal-03696252⟩

Serban Belinschi, Victor Magron, Victor Vinnikov. Noncommutative Christoffel-Darboux Kernels. Transactions of the American Mathematical Society, 2023, 376, pp.181-230. ⟨10.1090/tran/8648⟩. ⟨hal-03433869⟩

Mathias Serieye, Carolina Albea-Sanchez, Alexandre Seuret, Marc Jungers. Attractors and limit cycles of discrete-time switching affine systems : nominal and uncertain cases. Automatica, 2023, 149, pp.110691. ⟨10.1016/j.automatica.2022.110691⟩. ⟨hal-03110340v2⟩

Constantinos Kitsos, Mathieu Bajodek, Lucie Baudouin. Joint Coefficient and Solution Estimation for the 1D Wave Equation: An Observer-Based Solution to Inverse Problems. IEEE Transactions on Automatic Control, 2023, 68 (8), pp.4827 - 4840. ⟨10.1109/TAC.2022.3213625⟩. ⟨hal-03447113v3⟩

Didier Henrion, Felix Kirschner, Etienne de Klerk, Milan Korda, Jean-Bernard Lasserre, et al.. Revisiting semidefinite programming approaches to options pricing: complexity and computational perspectives. INFORMS Journal on Computing, 2023, 35 (2), pp.265-517. ⟨10.1287/ijoc.2022.1220⟩. ⟨hal-03429272v2⟩

Marianne Souaiby, Aneel Tanwani, Didier Henrion. Ensemble Approximations for Constrained Dynamical Systems using Liouville Equation. Automatica, 2023, 149, pp.110836. ⟨10.1016/j.automatica.2022.110836⟩. ⟨hal-03167458v3⟩

Isabelle Queinnec, Sophie Tarbouriech, Luca Zaccarian. Tour d’horizon sur les systèmes dynamiques hybrides. Les Techniques de l'Ingenieur, 2023, pp.Réf : S7434 v1. ⟨10.51257/a-v1-s7434⟩. ⟨hal-03946527⟩

R. Bertollo, A.R. Teel, Luca Zaccarian. Soft-Reset Control with Max-of-Quadratics Lyapunov Certificates. IEEE Transactions on Automatic Control, 2023, 68 (9), pp.5245 - 5257. ⟨10.1109/TAC.2022.3221684⟩. ⟨hal-03961277⟩

Victor Magron, Mohab Safey El Din, Trung-Hieu Vu. Sum of Squares Decompositions of Polynomials over their Gradient Ideals with Rational Coefficients. SIAM Journal on Optimization, 2023, 33 (1), ⟨10.1137/21M1436245⟩. ⟨hal-03312392⟩

Mathieu Bajodek, Frédéric Gouaisbaut, Alexandre Seuret. Necessary and sufficient stability condition for time-delay systems arising from Legendre approximation. IEEE Transactions on Automatic Control, 2023, 68 (10), pp.6262 - 6269. ⟨10.1109/TAC.2022.3232052⟩. ⟨hal-03435028v3⟩

Matteo Tacchi, Jean Bernard Lasserre, Didier Henrion. Stokes, Gibbs and volume computation of semi-algebraic sets. Discrete and Computational Geometry, 2023, 69 (1), pp.260-283. ⟨10.1007/s00454-022-00462-0⟩. ⟨hal-02947268v3⟩

Francesco Ferrante, Ricardo Sanfelice, Sophie Tarbouriech. Control design under actuator saturation and multi-rate sampling. Automatica, 2023, 148, pp.110767. ⟨10.1016/j.automatica.2022.110767⟩. ⟨hal-03946867⟩

Carla de Souza, Antoine Girard, Sophie Tarbouriech. Event-triggered Neural Network Control using Quadratic Constraints for Perturbed Systems. Automatica, 2023, 157, pp.111237. ⟨10.1016/j.automatica.2023.111237⟩. ⟨hal-04154871⟩

Franco Blanchini, Giulia Giordano, Francesco Riz, Luca Zaccarian. Solving nonlinear algebraic loops arising in input-saturated feedbacks. IEEE Transactions on Automatic Control, 2023, 68 (4), pp.2079-2093. ⟨10.1109/TAC.2022.3170858⟩. ⟨hal-04148146⟩

John Selby, Ana Belén Sainz, Victor Magron, Łukasz Czekaj, Michał Horodecki. Correlations constrained by composite measurements. Quantum, 2023, 7, pp.1080. ⟨10.22331/q-2023-08-10-1080⟩. ⟨hal-04117038⟩

Oliver Polo Mejia, Christian Artigues, Pierre Lopez, Lars Mönch, Virginie Basini. Heuristic and metaheuristic methods for the multi‐skill project scheduling problem with partial preemption. International Transactions in Operational Research, 2023, 30 (2), pp.858-891. ⟨10.1111/itor.13063⟩. ⟨hal-03475868⟩

Milan Korda, Victor Magron, Rodolfo Ríos-Zertuche. Convergence rates for sums-of-squares hierarchies with correlative sparsity. Mathematical Programming, 2023, ⟨10.1007/s10107-024-02071-6⟩. ⟨hal-04049383⟩

Riccardo Bonalli, Benoît Bonnet. First-Order Pontryagin Maximum Principle for Risk-Averse Stochastic Optimal Control Problems. SIAM Journal on Control and Optimization, 2023, 61 (3), pp.1881-1909. ⟨10.1137/22M1489137⟩. ⟨hal-03633263v5⟩

Books

Victor Magron, Jie Wang. Sparse Polynomial Optimization: Theory and Practice. World Scientific Press. 2023, Series on Optimization and Its Applications, 978-1-80061-294-5. ⟨10.1142/q0382⟩. ⟨hal-03760501⟩

Book sections

Mélody Mailliez, Hugo Chevroton, Cyril Briand, Philippe Truillet, Céline Lemercier. Stepping stone to smarter supervision: a human-centered multidisciplinary framework. Chaudhery Mustansar Hussain; Daniel Rossit. Designing Smart Manufacturing Systems, chapter 4, Elsevier, pp.89-118, 2023, ⟨10.1016/B978-0-32-399208-4.00011-8⟩. ⟨hal-04181324⟩

Jean-Bernard Lasserre. Polynomial Optimization, Certificates of Positivity, and Christoffel Function. Michal Kočvara; Bernard Mourrain; Cordian Riener. Polynomial Optimization, Moments, and Applications, Springer, pp.1-20, 2023. ⟨hal-04076663⟩

Conference papers

Yoni Lahana, Mauro Mancini, Dimitri Peaucelle, Elisa Capello, Hélène Evain. Comparison of Adaptive Control Laws on a Satellite Attitude Control Benchmark. Conference on Control, Decision and Information Technologies, Jul 2023, Rome, Italy. ⟨hal-04088506⟩

Camille Coquand, Yannick Pencolé, Audine Subias. Diagnosabilization of Time Petri net for timed fault. IFAC World COngress, Jul 2023, Yokoama, Japan. pp.8648-8653, ⟨10.1016/j.ifacol.2023.10.041⟩. ⟨hal-04075303⟩

Carla Juvin, Emmanuel Hebrard, Laurent Houssin, Pierre Lopez. An Efficient Constraint Programming Approach to Preemptive Job Shop Scheduling. 29th International Conference on Principles and Practice of Constraint Programming, Aug 2023, Toronto ( CA ), Canada. pp.19, ⟨10.4230/LIPIcs.CP.2023.19⟩. ⟨hal-04245373⟩

Silvia Di Girolamo, Filippo d'Ippolito, Massimiliano Luna, Marcello Pucci, Antonino Sferlazza, et al.. Control of a Multi-Input Converter Using Dynamic Input Allocation. IECON 2023- 49th Annual Conference of the IEEE Industrial Electronics Society, Oct 2023, Singapore, Singapore. pp.1-6, ⟨10.1109/IECON51785.2023.10312047⟩. ⟨hal-04776128⟩

Manon Doré, Yassine Ariba, Germain Garcia. Observer-based Switched Control of the Three Level Neutral Point Clamped Rectifier. Conference on Decision and Control CDC 2023, Dec 2023, Singapore (SG), Singapore. ⟨10.1109/CDC49753.2023.10383201⟩. ⟨hal-04343704⟩

Julien Ferry, Ulrich Aïvodji, Sébastien Gambs, Marie-José Huguet, Mohamed Siala. Exploiter l'équité d'un modèle d'apprentissage pour reconstruire les attributs sensibles de son ensemble d'entraînement. Rencontres des Jeunes Chercheurs en Intelligence Artificielle (RJCIA/PFIA 2023), Jul 2023, Strasbourg, France. ⟨hal-04190265⟩

Carla Juvin, Laurent Houssin, Pierre Lopez. Hybrid Methods to Solve the Two-Stage Robust Flexible Job-Shop Scheduling Problem with Budgeted Uncertainty. 12th International Conference on Operations Research and Enterprise Systems (ICORES), Feb 2023, Lisbonne, Portugal. pp.135-142. ⟨hal-03963343⟩

Julien Ferry, Ulrich Aïvodji, Sébastien Gambs, Marie-José Huguet, Mohamed Siala. Exploiting Fairness to Enhance Sensitive Attributes Reconstruction. First IEEE Conference on Secure and Trustworthy Machine Learning, Feb 2023, Raleigh, North Carolina, United States. ⟨10.1109/SaTML54575.2023.00012⟩. ⟨hal-03766710v2⟩

Julien Rouzot, Christian Artigues, Philippe Garnier, Emmanuel Hebrard, Pierre Lopez. Global constraints for scheduling data transfer in space missions. 13th International Workshop on Planning and Scheduling for Space (IWPSS 2023), Steve Chien, Juan Manuel Delfa and Tiago Stegun Vaquero, Jul 2023, Prague, Czech Republic. pp.93-95. ⟨hal-04171352⟩

Anna Sztyber, Elodie Chanthery, Louise Travé-Massuyès. Benchmark for Fault Diagnosis of Water Distribution Network. The 34th International Workshop on Principles of Diagnosis (DX'23), PARC and the Silicon Austria Labs (SAL)., Sep 2023, Loma Mar, United States. ⟨hal-04327789⟩

Carla Juvin, Laurent Houssin, Pierre Lopez. Approche hybride multi-étape pour la résolution du problème de job-shop flexible robuste avec budget d'incertitude. 24e congrès de la Société française de recherche opérationnelle et d'aide à la décision (ROADEF 2023), Rennes School of Business, Feb 2023, Rennes, France. ⟨hal-03998579⟩

Audine Subias, Louise Travé-Massuyès, Tom Obry. DyClee-N&C: a clustering algorithm for heterogeneous data based situation assessment. IFAC World Congress, Jul 2023, Yokohama, Japan. ⟨hal-04268806⟩

Julien Rouzot, Christian Artigues, Philippe Garnier, Emmanuel Hebrard, Pierre Lopez. Une contrainte globale pour l'ordonnancement des transferts de données dans les missions spatiales. Journées Francophones de Programmation par Contraintes (JFPC 2023), Jul 2023, Strasbourg, France. pp.115-119. ⟨hal-04171325⟩

Mateusz Skomra. Signed Tropicalizations of Convex Semialgebraic Sets. Extended Abstracts presented at the 25th International Symposium on Mathematical Theory of Networks and Systems MTNS 2022, Sep 2022, Bayreuth, Germany. pp.697-700, ⟨10.15495/EPub_UBT_00006809⟩. ⟨hal-04273455⟩

Yassine Ariba, Frédéric Gouaisbaut, Flavien Deschaux, François Roux, François Dugué. Experimental results for a pressure reducer control with a modular actuator. 62nd IEEE Conference on Decision and Control (CDC), Dec 2023, Singapore, Singapore. ⟨10.1109/CDC49753.2023.10383394⟩. ⟨hal-04190427v2⟩

Christine Leterrier, Claire Bonnefous, Jarkko Niemi, Lucia Rocchi, Giuditta Meloni, et al.. Welfare barriers and levers for improvement in organic and low-input outdoor pig and poultry production systems. 74. Annual meeting of the european federation of animal science (EAAP 2023), EAAP, Aug 2023, Lyon, France. pp.731. ⟨hal-04198015⟩

Emir Demirović, Emmanuel Hebrard, Louis Jean. Blossom: an Anytime Algorithm for Computing Optimal Decision Trees. International Conference on Machine Learning, Jul 2023, Honolulu, United States. ⟨hal-04108022⟩

Victor Magron. Sparse polynomial optimization: theory and practice. 17th International Symposium on Operations Research in Slovenia, Sep 2023, Bled, Slovenia. ⟨hal-04719292⟩

Arthur S Fagundes, João M Gomes da Silva Jr, Sophie Tarbouriech. Stability analysis of sampled-data systems with sector-bounded input nonlinearity. The 22nd World Congress of the International Federation of Automatic Control, Jul 2023, Porto Alegre, Brazil. pp.9812 - 9817, ⟨10.1016/j.ifacol.2023.10.400⟩. ⟨hal-04361603⟩

Carla Juvin, Laurent Houssin, Pierre Lopez. Constraint programming for the robust two-machine flow-shop scheduling problem with budgeted uncertainty. 20th International Conference on the Integration of Constraint Programming, Artificial Intelligence, and Operations Research (CPAIOR), May 2023, Nice, France. pp.354-359. ⟨hal-03963365⟩

Florent Teichteil-Königsbuch, Guillaume Povéda, Guillermo González de Garibay Barba, Tim Luchterhand, Sylvie Thiébaux. Fast and Robust Resource-Constrained Scheduling with Graph Neural Networks. 33rd International Conference on Automated Planning and Scheduling (ICAPS), Jul 2023, Prague, Czech Republic. ⟨hal-04141504⟩

Louise Travé-Massuyès. Leveraging the properties of the Christoffel function for anomaly detection in data stream. 20 years of the Institute for Software Technology at TU Graz, Institute for Software Technology at TU Graz, Dec 2023, Graz, Austria. ⟨hal-04795340⟩

Menglin He, Xue Han, Nathalie Di Miceli Raimondi, Michel Cabassud, Boutaib Dahhou, et al.. The Simplified Modeling and Experimental Verification of a Heat Exchanger/Reactor*. IEEE 11th International Conference on Systems and Control (ICSC 2023), Dec 2023, Sousse, Tunisia. pp.677-682, ⟨10.1109/ICSC58660.2023.10449866⟩. ⟨hal-04541196⟩

Quoc Hung Lu, Soheib Fergani, Carine Jauberthie. Fault detection using Enhanced Adaptive degrees of freedom χ2-statistics method for Linear systems with mixed uncertainties. The 22nd World Congress of the International Federation of Automatic Control, Jul 2023, Yokohama, Japan. ⟨hal-04069624⟩

Xue Han, Menglin He, Nathalie Di Miceli Raimondi, Michel Cabassud, Boutaib Dahhou. Distributed adaptive observer-based Fault Diagnosis for an Intensified Heat Exchanger/Reactor. 31st Mediterranean Conference on Control and Automation (MED 2023), Jun 2023, Limassol, Cyprus. ⟨hal-04827116⟩

Alessandro Bosso, Miguel Mannes Hillesheim, Marc Cousineau, Luca Zaccarian. Nonlinear Stability Analysis of Distributed Self-Interleaving for Driving Signals in Multicellular Converters. 2023 62nd IEEE Conference on Decision and Control (CDC), Dec 2023, Singapore, Singapore. pp.3574-3579, ⟨10.1109/CDC49753.2023.10383935⟩. ⟨hal-04719389⟩

Victor Magron. Exploiting sparsity in polynomial optimization. Journées nationales de calcul formel (JNCF), Mar 2023, Marseille (CIRM, Centre International de Rencontres Mathématiques), France. ⟨hal-04719298⟩

Mario Gauvrit, Christophe Prieur, Sophie Tarbouriech. A note on the wave equation controlled with a dynamic saturating boundary control. NOLCOS 2022 - 12th IFAC Symposium on Nonlinear Control Systems (NOLCOS'22), Jan 2023, Canberra, Australia. pp.108-113, ⟨10.1016/j.ifacol.2023.02.019⟩. ⟨hal-04159866⟩

Alban Puech, Tristan Rigaut, Adrien Le Franc, William Templier, Jean-Christophe Alais, et al.. Controlling Microgrids Without External Data: A Benchmark of Stochastic Programming Methods. IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE 2023), Oct 2023, Grenoble, France. ⟨10.1109/ISGTEUROPE56780.2023.10407934⟩. ⟨hal-04083666v3⟩

Quoc Hung Lu, Soheib Fergani, Carine Jauberthie. Fault detection combining adaptive degrees of freedom χ2-statistics and interval approach for nonlinear systems. The 22nd World Congress of the International Federation of Automatic Control (IFAC), Jul 2023, Yokohama, Japan. ⟨hal-04069589⟩

Xue Han, Mondher Farza, Mohammed M'Saad, Boutaib Dahhou. Suitable Temperatures and Reaction Heats Estimation within an Intensified Heat Exchanger/Reactor. IEEE 11th International Conference on Systems and Control (ICSC 2023), Dec 2023, Sousse, Tunisia. pp.177-182, ⟨10.1109/ICSC58660.2023.10449787⟩. ⟨hal-04541167⟩

Dimitri Peaucelle. Exploring robust structured static output feedback design. Workshop on Uncertain Dynamical Systems, Jul 2023, Kyoto, Japan. ⟨hal-04745661⟩

Olga Yufereva, Aneel Tanwani. Transport Inspired Particle Filters with Poisson-Sampled Observations in Gaussian Setting. 2023 62nd IEEE Conference on Decision and Control (CDC), Dec 2023, Singapore, Singapore. pp.7695-7700, ⟨10.1109/CDC49753.2023.10384088⟩. ⟨hal-04489396⟩

Matthieu Masson, Denis Arzelier, Mioara Joldes, Bruno Revelin, Jérôme Thomassin. Multi-maneuvers algorithms for multi-risk collision avoidance via nonconvex quadratic optimization. IFAC World Congress 2023, Jul 2023, Yokohama, Japan. ⟨hal-03847541⟩

Louise Travé-Massuyès. Leveraging the properties of the Christoffel function for anomaly detection in data streams. POP23 - Future Trends in Polynomial OPtimization, LAAS-CNRS, Toulouse, Nov 2023, Toulouse, France. ⟨hal-04795310⟩

Manon Dore, Yassine Ariba, Germain Garcia. General methodology for observer-based control of power electronic converters with measured perturbations. Conference on Control Technology and Applications CCTA 2023, Aug 2023, Bridgetown, Barbados. ⟨hal-04219916⟩

Ghassen Cherif, Dimitri Lefebvre. Modelling and optimization approaches for advanced manufacturing systems. ICIEA-EU 2023: 2023 The 10th International Conference on Industrial Engineering and Applications, Jan 2023, Rome, Italy. pp.84-90, ⟨10.1145/3587889.3587903⟩. ⟨hal-04468991⟩

Edgar Hernando Sepúlveda Oviedo, Louise Travé-Massuyès, Audine Subias, Marko Pavlov, Corinne Alonso. Detection and classification of faults aimed at preventive maintenance of PV systems.. XI Congreso Internacional de Ingeniería Mecánica, Mecatrónica y Automatización 2023, Universidad Nacional de Colombia, Apr 2023, Carthagène, Colombia. ⟨hal-04125988⟩

Carine Jauberthie, Louise Travé-Massuyès, Nathalie Verdière. Identifiabilité ensembliste et détection de fautes au travers de l'estimation paramétrique. 1er congrès de la SAGIP, Jun 2023, Marseiile, France. ⟨hal-04116243⟩

Yassine Ariba, Frédéric Gouaisbaut. A singular perturbation approach for the control of electromagnetic actuators. 22nd IFAC World Congress, Jul 2023, Yokohama, Japan. pp.6057-6062, ⟨10.1016/j.ifacol.2023.10.661⟩. ⟨hal-04056821v2⟩

Corentin Boennec, Bruno Sareni, Sandra Ulrich Ngueveu. Robust Design of Microgrids using Component Models with Different Level of Accuracy. OIPE 2023 (17th International Workshop on Optimization and Inverse Problems in Electromagnetism), Sep 2023, Graz, Austria. ⟨hal-04367497⟩

Guillaume Povéda, Nahum Alvarez, Christian Artigues. Partially Preemptive Multi Skill/Mode Resource-Constrained Project Scheduling with Generalized Precedence Relations and Calendars. 29th International Conference on Principles and Practice of Constraint Programming (CP 2023), Aug 2023, Toronto, Canada. ⟨10.4230/LIPIcs.CP.2023.31⟩. ⟨hal-04217223⟩

Edgar Hernando Sepúlveda Oviedo, Louise Travé-Massuyès, Audine Subias, Marko Pavlov, Corinne Alonso. DTW K-Means clustering for fault detection in photovoltaic modules. XI Congreso Internacional de Ingeniería Mecánica, Mecatrónica y Automatización 2023, Apr 2023, Carthagène, Colombia. ⟨hal-04125983⟩

Tychique Nzalalemba Kabwangala, Jean-Pierre Fradin, Yassine Ariba, Alexandre Marie, Frédéric Gouaisbaut. Observer based junction temperature estimation: 3D simulations and experimentations. Therminic, 29th international workshop on Thermal Investigations of ICs and Systems, Sep 2023, Budapest, Hungary. ⟨10.1109/THERMINIC60375.2023.10325885⟩. ⟨hal-04221697⟩

Alexandre Heintzmann, Christian Artigues, Pascale Bendotti, Sandra Ulrich Ngueveu, Cécile Rottner. Efficient exact A* algorithm for the single unit hydro unit commitment problem. 18th Conference on Computer Science and Intelligence Systems, Sep 2023, Warsaw, Poland. pp.527-537, ⟨10.15439/2023F5158⟩. ⟨hal-04112945v3⟩

Dorian Voydie, Louis Goupil, Elodie Chanthery, Louise Travé-Massuyès, Sébastien Delautier. Machine Learning Based Fault Anticipation for 3D Printing. 22nd World Congress of the International Federation of Automatic Control (IFAC 2023), IFAC: International Federation of Automatic Control, Jul 2023, Yokohama, Japan. ⟨hal-04268835⟩

Cyrille Briand, Arthur Bit-Monnot, Adrien Deckx van Ruys. Planification prévisionnelle de véhicules autonomes pour la logistique interne de systèmes de production. 24ème congrès de la Société Française de Recherche Opérationnelle et d'Aide à la Décision ROADEF 2023, Nadjib Brahimi, Feb 2023, Rennes, France. ⟨hal-04249513⟩

Philipp Braun, Marc Jungers, Luca Zaccarian. Stabilization using shifted equilibria for saturated discrete-time linear systems. 12th IFAC Symposium on Nonlinear Control Systems, NOLCOS 2023, Jan 2023, Camberra, Australia. ⟨10.1016/j.ifacol.2023.02.005⟩. ⟨hal-03877627⟩

Mathieu Bajodek, Daniele Astolfi. Comparison between different continuous-time realizations based on the tau method of a nonlinear repetitive control scheme. 62nd IEEE Conference on Decision and Control (CDC 2023), Dec 2023, Singapour, Singapore. ⟨10.1109/CDC49753.2023.10384072⟩. ⟨hal-04178964⟩

Louis Goupil, Elodie Chanthery, Louise Travé-Massuyès, Sébastien Delautier. Tree based diagnosis enhanced with meta knowledge. 34th International Workshop on Principles of Diagnosis (DX'23), Sep 2023, Loma Mar, United States. ⟨hal-04186400⟩

Samuele Zoboli, Andreu Cecilia, Ulysse Serres, Daniele Astolfi, Vincent Andrieu. LMI conditions for k-contraction analysis: a step towards design. 62nd IEEE Conference on Decision and Control (CDC 2023), IEEE, Dec 2023, Singapore, Singapore. ⟨10.1109/CDC49753.2023.10383436⟩. ⟨hal-04304423⟩

Le Toan Duong, Louise Travé-Massuyès, Audine Subias, Christophe Merle. Remaining cycle time prediction with Graph Neural Networks for Predictive Process Monitoring. 8th International Conference on Machine Learning Technologies (ICMLT 2023), Mar 2023, Stockholm, Sweden. 7 p., ⟨10.1145/3589883.3589897⟩. ⟨hal-04093621⟩

Master thesis

Hannes van Overloop. Joint task sequencing and motion planning for a mobile manipulator-robot. Operations Research [math.OC]. 2023. ⟨hal-04452267⟩

Patents

Edgar Hernando Sepúlveda-Oviedo, Louise Travé-Massuyès, Audine Subias, Marko Pavlov, Corinne Alonso. Méthode de détection de défauts dans une installation photovoltaïque. France, N° de brevet: FR2310256. Rapport LAAS n° 23666. 2023. ⟨hal-04773333⟩

Flavien Deschaux, Yassine Ariba, Damien de Seze, Frédéric Gouaisbaut, François Dugué. Procédé de commande d’un actionneur éléctromagnétique d’un détendeur, et actionneur et détendeur configuré pour mettre en œuvre ledit procédé. France, N° de brevet: FR3121193. Rapport LAAS n° 23087. 2023, https://data.inpi.fr/brevets/FR3121193. ⟨hal-04054668⟩

Bolting Jan, Soheib Fergani. CONSTRAINED ZONOTOPE ENCLOSING A STATE REPRESENTING MOTION OF AT LEAST ONE MOBILE TARGET GOVERNED BY A NONLINEAR MODEL. France, Patent n° : US20220326389A1. 2023. ⟨hal-04845835⟩

Proceedings

Jared Miller, Milan Korda, Victor Magron, Mario Sznaier. Peak Estimation of Time Delay Systems using Occupation Measures. 2023 62nd IEEE Conference on Decision and Control (CDC), IEEE, pp.5294-5300, 2023, ⟨10.1109/CDC49753.2023.10384165⟩. ⟨hal-04047493⟩

Przemysław Koprowski, Victor Magron, Tristan Vaccon. Pourchet's theorem in action: decomposing univariate nonnegative polynomials as sums of five squares. ISSAC 2023: International Symposium on Symbolic and Algebraic Computation 2023, ACM, pp.425-433, 2023, ⟨10.1145/3597066.3597072⟩. ⟨hal-03976836⟩

Reports

Théo Le Brun, Marie-José Huguet, Sandra Ulrich Ngueveu. Un aperçu du e-commerce socialement-responsable français. Toulouse INP; LAAS - CNRS. 2023. ⟨hal-04214507v2⟩

Théo Le Brun, Marie-José Huguet, Sandra Ulrich Ngueveu. Un aperçu du e-commerce éco-responsable français. Toulouse INP; LAAS - CNRS. 2023. ⟨hal-04142062v3⟩

Dimitri Peaucelle, Damien Trentesaux, Gülgün Alpan, Romain Postoyan, Jean Auriol, et al.. Groupement de Recherche MACS - Bilan 2019-2023 et Projet 2024-2028. 2023. ⟨hal-04246559⟩

Charles-Maxime Gauriat, Yannick Pencolé, Pauline Ribot, Gregory Brouillet. An experimental setup for learning models for the RUL estimation of bearings in rotary machine tools: towards the learning of more interpretable models. 2023. ⟨hal-04715967⟩

Preprints, Working Papers, ...

Didier Henrion, Milan Korda, Jean-Bernard Lasserre. POLYNOMIAL ARGMIN FOR RECOVERY AND APPROXIMATION OF MULTIVARIATE DISCONTINUOUS FUNCTIONS. 2023. ⟨hal-03986252v2⟩

Igor Klep, Victor Magron, Jurij Volčič. Sums of squares certificates for polynomial moment inequalities. 2023. ⟨hal-04125262⟩

Bernard Brogliato, Aneel Tanwani. Feedback Interconnections of Passive Linear Cone Complementarity Systems. 2024. ⟨hal-04137144v2⟩

Ngoc Hoang Anh Mai, Victor Magron. Sums of squares representations on singular loci. 2023. ⟨hal-04023980⟩

Victor Magron. Exploiting sparsity in polynomial optimization. École thématique. Luminy, France. 2023. ⟨hal-04193936⟩

Jean-Bernard Lasserre. The Moment-SOS hierarchy: Applications and related topics. 2023. ⟨hal-04201167⟩

Alexandre Heintzmann, Pascale Bendotti, Cécile Rottner. Two-phase Branch & Cut for the Symmetric Weight Matrix Knapsack polytope. 2023. ⟨hal-03992007⟩

Didier Henrion, Milan Korda, Martin Kružík, Rodolfo Rios-Zertuche. Occupation measure relaxations in variational problems: the role of convexity. 2023. ⟨hal-04118080⟩

Lucie Baudouin, Maya de Buhan, Emmanuelle Crépeau, Julie Valein. Carleman-Based Reconstruction Algorithm on a wave Network. 2023. ⟨hal-04361363⟩

Didier Henrion, Maria Infusino, Salma Kuhlmann, Victor Vinnikov. Infinite-dimensional moment-SOS hierarchy for nonlinear partial differential equations. 2024. ⟨hal-04117218v2⟩

Carla Juvin, Laurent Houssin, Pierre Lopez. Decomposition methods for the preemptive Flexible Job-Shop Scheduling Problem. 2023. ⟨hal-04243944⟩

Mathieu Bajodek, Hugo Lhachemi, Giorgio Valmorbida. Stability properties for two coupled reaction-diffusion equations. 2023. ⟨hal-03861580v2⟩

Didier Henrion. Geometry of exactness of moment-SOS relaxations for polynomial optimization. 2023. ⟨hal-04258249v3⟩

Julien Ferry, Gabriel Laberge, Ulrich Aïvodji. Learning Hybrid Interpretable Models: Theory, Taxonomy, and Methods. 2023. ⟨hal-04010590⟩

Alexandre Seuret, Sophie Tarbouriech. Robust data-driven control design for linear systems subject to input saturation. 2024. ⟨hal-04203689⟩

Simone Mariano, Romain Postoyan, Luca Zaccarian. Finite-time stability properties of Lur'e systems with piecewise continuous nonlinearities. 2023. ⟨hal-03987552⟩

Didier Henrion, Simone Naldi, Mohab Safey El Din. Algebraic certificates for the truncated moment problem. 2023. ⟨hal-03987123⟩

Mathieu Bajodek, Fernando Castaños, Sabine Mondié. State prediction using a high-gain distributed scheme. 2023. ⟨hal-04267738⟩

Yannick Pencolé. Notes de cours: Analyse, Simulation et Commande de systèmes (max,+)-linéaires.. Master. Module Controle et Simulation (partie 1), Université Paul Sabatier, Toulouse, France. 2023, pp.58. ⟨hal-04775880⟩

THESIS / HDR

2024

Charlotte Lacoquelle, Thèse: Détection d'anomalies dans les séries temporelles altérées - Application à la surveillance des robots industriels

Nicola Zaupa, Thèse: Cycles Limites Hybrides : de la théorie à la pratique dans les convertisseurs résonnants

Santiago Pantano-Calderón, Thèse: Algorithmes de conception non quadratiques pour les systèmes linéaires soumis à saturation d'entrée

Louis Goupil, Thèse: Apprentissage machine guidé par des connaissances pour le diagnostic

Olga Iufereva, Thèse: Algorithmes de filtrage avec les observations distribuées par Poisson

Alexandre Heintzmann, Thèse: Modèles et algorithmes pour l'optimisation de la production hydro-électrique

2023

Louis Rivière, Thèse: Représentation compacte d'ensemble de solutions pour l'ordonnancement sous incertitude

Vit Cibulka, Thèse: L'approche de Koopman et moment-sum-of-squares pour le contrôle : méthodes de calcul et applications

Camille Coquand, Thèse: Diagnosticabilité et diagnosticabilisation de motifs temporels dans les réseaux de Petri temporels

Lucas Dal Bosco, Thèse: Dosimétrie basée sur l’imagerie portale par apprentissage de réseaux de neurones convolutifs pour l’assurance qualité spécifique au patient en radiothérapie externe.

Lucas Dal Bosco, Thèse: Dosimétrie basée sur l’imagerie portale par apprentissage de réseaux de neurones convolutifs pour l’assurance qualité spécifique au patient en radiothérapie externe.

Aloïs Duguet, Thèse: Approximation linéaire par morceaux de fonctions de deux variables avec erreur bornée pour la résolution de problèmes d'optimisation non linéaire mixte en nombres entiers

Florent Koudohode, Thèse: Commande basée évènement pour quelques équations aux dérivées partielles

Julien Ferry, Thèse: Adresser l’interprétabilité, l’équité et la protection de la vie privée en apprentissage machine au travers des méthodes d’optimisation combinatoire

Carla Juvin, Thèse: Méthodes hybrides pour l'ordonnancement disjonctif avec flexibilité de ressources et considération de robustesse

Kévin Ducharlet, Thèse: Détection d'anomalies dans les flux de données pour une application dans les réseaux de capteurs

Antoine Boche, Thèse: Étude de la durabilité des micro-réseaux par un modèle systémique basé sur la théorie de la modélisation et de la simulation

Le Toan Duong, Thèse: Extraction de connaissances pour l'optimisation des processus de production par process mining

Corbinian Schlosser, Thèse: Parcimonie et optimisation convexe pour les systèmes dynamiques

Alexandre Gaffet, Thèse: Approches de machine learning pour le diagnostic de processus de production automobile

2022

Hao Hu, Thèse: Interpretable Machine Learning Models via Maximum Boolean Satisfiability

Tong Chen, Thèse: Vérification de la robustesse des réseaux de neurones à l'aide de l'optimisation polynomiale

Amaury Vignolles, Thèse: Apprentissage de modèles pour la gestion de santé de systèmes hybrides sous incertitudes

Ngoc Hoang Anh Mai, Thèse: Optimisation polynomiale pratique grâce à des certificats de positivité avec et sans dénominateurs

Mathieu Bajodek, Thèse: Analyse de stabilité de systèmes linéaires EDO-EDP interconnectés

Valentin Antuori, Thèse: Guider la recherche arborescente pour la résolution de problèmes industriels : apprentissage par renforcement et méthodes de Monte Carlo

Tom Portoleau, Thèse: Représentations discrètes pour l’ordonnancement et la planification robustes

Quentin Fabry, Thèse: Ordonnancement de camions dans une plateforme logistique : complexité, méthodes de résolution et incertitudes

Léa Blaise, Thèse: Modélisation et résolution de problèmes d’ordonnancement au sein du solveur d’optimisation mathématique LocalSolver

Claire Paya, Thèse: Détection des dérives temporelles pour le pilotage de flux de production dans l'industrie des semiconducteurs

Quoc Hung Lu, Thèse: Filtrage à incertitudes stochastiques et bornées : application au diagnostic actif en automobile

2021

Frédéric Chatrie Roudier, Thèse: Dosimétrie in-vivo et contrôle qualité en radiothérapie externe par réseaux de neurones

Edouard Villain, Thèse: Utilisation de l'intelligence artificielle pour l'aide au diagnostic des patients atteints de pathologies neuro dégénératives

Mathias Serieye, Thèse: Contributions à la stabilisation des systèmes à commutation affine

Marianne Souaiby, Thèse: Fonctions de Lyapunov et approximations d'ensemble pour les systèmes contraints utilisant la programmation semi-définie

Thomas Conord, Thèse: Contrôle robuste des systèmes variant dans le temps : application au contrôle d'attitude modélisée par quaternion

Menglin He, Thèse: Commande tolérante aux fautes des systèmes non linéaires basée sur l'approche multi-modèles

Matteo Tacchi, Thèse: Hiérarchie moments-SOS pour approximation ensembliste à grande échelle. Application à l'analyse de stabilité transitoire des systèmes électriques.

Victor Magron, Habilitation à diriger des recherches: The quest of modeling, certification and efficiency in polynomial optimization

Xue Han, Thèse: Diagnostic basé sur les observateurs et commande tolérante aux fautes des systèmes non linéaires

2020

Valentin Bouziat, Thèse: Gestion des aléas dans un système multi-robots

Matteo Della Rossa, Thèse: Fonctions de Lyapunov non-lisses pour l'analyse de stabilité de systèmes hybrides

Flavien Deschaux, Thèse: Analyse et synthèse du système de commande d’un détendeur électroniquepour applications spatiales

Tom Obry, Thèse: Apprentissage numérique et symbolique pour le diagnostic et la réparation automobile

Alexandre Sahuguède, Thèse: Un algorithme de découverte de chroniques pertinentes pour le diagnostic par identification et reconstitution

2019

Estele Glize, Thèse: Méthodes exactes pour les problèmes combinatoires bi-objectif : Application sur les problèmes de tournées de véhicules

Simon Belieres, Thèse: Programmation mathématiques pour la plannification tactique du transport dans une chaîne logistique multi-produits

Oliver Polo Mejia, Thèse: Approche par recherche opérationnelle de l'optimisation du fonctionnement d'un laboratoire en milieu nucléaire

Florent Bréhard, Thèse: Certified numerics in function spaces : polynomial approximations meet computer algebra and formal proof

Sabrina Hadjeras, Thèse: Commande hybride pour des convertisseurs de puissance

Matthieu Barreau, Thèse: Analyse de stabilité de systèmes différentiels ordinaires couplés avec une équation des ondes : application aux mécanismes de forage

Mioara Maria Joldes, Habilitation à diriger des recherches: Algorithmes symboliques-numeriques validés et applications au domaine spatial

Matteo Cocetti, Thèse: Rétroactions non linéaires et hybrides avec systèmes linéaires à temps continu

2018

Pierre-Antoine Morin, Thèse: Planification et ordonnancement de projets sous contraintes de ressources complexes

Idir Hamaz, Thèse: Méthodes d'optimisation robuste pour les problèmes d'ordonnancement cyclique

Mohammed Safi, Thèse: Stabilité de Lyapunov de systèmes couplés impliquant une équation de transport

Paulo Ricardo Arantes Gilz, Thèse: Algorithmes de commande embarqués et validés pour le rendez-vous spatial

Tillmann Weisser, Thèse: Moments et polynômes positifs pour le calcul d'approximations et de solutions généralisées

Yannick Pencolé, Habilitation à diriger des recherches: Diagnostic : étude d’un raisonnement complexe et multi-dimensionnel

Mikael Capelle, Thèse: Optimisation pour les communications optiques dans les systèmes d’observation de la Terre

Elodie Chanthery, Habilitation à diriger des recherches: Vers des systèmes plus autonomes : contributions autour de la tâche de diagnostic dans une architecture embarquée

Pierre Coupechoux, Thèse: Codes et jeux de soustraction et de poursuite dans les graphes

Fabien Niel, Thèse: Modélisation et contrôle d'une aile en présence d'oscillations aéroélastiques de grande amplitude et à faible nombre de Reynolds

Ulrich Matchi Aïvodji, Thèse: Technologies respectueuses de la vie privée pour le covoiturage

2017

Alexandre Seuret, Habilitation à diriger des recherches: Contributions à l'analyse de la stabilité et au contrôle des systèmes en réseau

Yun He, Thèse: Problèmes de tournée avec prise en compte explicite de la consommation d'énergie

Tuan Anh Tran, Thèse: Cadre unifié pour la modélisation des incertitudes statistiques et bornées : application à la détection et isolation de défauts dans les systèmes dynamiques incertains par estimation

John William Vásquez Capacho, Thèse: Gestion d’alarmes basée sur des chroniques

Harmonie Leduc, Thèse: Contrôle adaptatif robuste. Application au contrôle d'attitude de satellites

Laura Sofia Urbina, Thèse: Méthodes de guidage-contrôle robuste pour la phase d'approche entre deux véhicules orbitaux avec couplage des mouvements de translation et de rotation

Christophe Louembet, Habilitation à diriger des recherches: Contributions au guidage pour le rendez-vous spatial par résolution du problème de commande optimale impulsionnelle

2016

Clément Carbonnel, Thèse: Algorithmes paramétrés pour des problèmes de satisfaction de contraintes presque traitables

Saïd Zabi, Thèse: Modélisation et commande de l’anesthésie en milieu clinique

Thomas Monrousseau, Thèse: Développement du système d'analyse des données recueillies par les capteurs et choix du groupement de capteurs optimal pour le suivi de la cuisson des aliments dans un four

Laura Dal Col, Thèse: Etudes des techniques de contrôle distribué pour l'analyse et la synthèse pour les systèmes multi-agents avec information limitée

Carine Jauberthie, Habilitation à diriger des recherches: Estimation des systèmes dynamiques incertains et des propriétés connexes. Application à la surveillance de la santé

Margaux Nattaf, Thèse: Ordonnancement sous contraintes d’énergie

Gregoire Scano, Thèse: Calcul d'itinéraires multiples et de trajets synchronisés dans des réseaux de transport multimodaux

Leticia Gloria Vargas Suarez, Thèse: Un opérateur de programmation dynamique pour les méta-heuristiques pour résoudre les problèmes de tournées de véhicules avec des visites optionnelles

Nadia Chaabane, Thèse: Recherche de flots stables dans des réseaux de transport multi-agents

2015

Elisa Roux, Thèse: Développement d'un outil d'aide au diagnostic pour la production de maïs permettant la réduction de la consommation en eaux d'irrigation et en traitements phytosanitaires

Olesia Mokrenko, Thèse: Gestion de l'énergie d'un réseau de capteurs sans fil au niveau de l'application

Francesco Ferrante, Thèse: Sur la quantification et l'intermittence de mesures dans les systèmes de commande: stabilité, stabilisation et estimation d'état

Simone Naldi, Thèse: Algorithmes exacts pour les variétés déterminantielles et la programmation semi-définie

Mohamed Siala, Thèse: Recherche, propagation et apprentissage dans les problèmes de séquencement et d'ordonnancement

Mathieu Poquet, Thèse: Une contribution à l'analyse et la modélisation des émissions de NO et N2O pendant nitritation

DEPARTMENT NEWS

26.04.24 PRESTO project wins IEA 2023 call - CNRS Sciences informatiques

MORE NEWS


OTHERS DEPARTMENTS

OF LAAS-CNRS

in one clic

picto

Job offers
picto

Media library
picto

People
picto

School

LAAS-CNRS

7, av. du colonel Roche
BP 54200
31031 Toulouse cedex 4
France

GPS : 43.563545, 1.476923

Tél :

LinkedIn Twitter
+ The Lab + Research + Platforms + Training for and to research + Partnership + News

LAAS-CNRS

is associated to 5 founding members
of COMUE Université de Toulouse
Université<br>Toulouse
Université Toulouse III Paul Sabatier (UPS)
Institut national<br>des sciences appliquées<br>de Toulouse<br>(INSA)
Institut national<br>polytechnique<br>de Toulouse<br>(INPT)
Université<br>Toulouse- Jean Jaurès<br>(UT2J)
Université<br>Toulouse I Capitole<br>(UT1)
Log in Intranet Legal notes