Polynomial OPtimization
- pop -
HEAD
The team currently investigates the following research topics:
Structure exploitation
How to make the Moment-SOS hierarchy more tractable?
Dynamical systems with algebraic data
Extension of the Moment-SOS hierarchy to dynamical systems
Noncommutative POP
Polynomial optimization in non-commuting variables
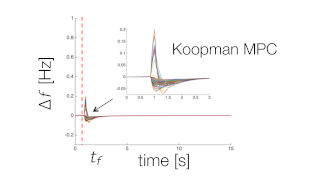
Koopman operators, data-driven control
for control of complex nonlinear dynamical systems
Tropical geometry
Connections between tropical geometry and positivity certificates
Algebraic methods for validated optimization
Going from approximate to exact certificates
Application fields
Quantum, learning and energy
Christoffel-Darboux (CD) kernels
Borrowed to approximation theory
Head
Scientific executive
Postdoctoral
PhD
Latest publications
2025
Journal articles
Reports
Preprints, Working Papers, ...
Victor Magron. Convergence rates for polynomial optimization on set products. 2025. ⟨hal-05086019⟩
Didier Henrion. Maximal entropy in the moment body. 2025. ⟨hal-05092147v2⟩
Jean B Lasserre. A laplace duality for integration. 2025. ⟨hal-04970360v3⟩
2024
Journal articles
Books
Conference papers
Other documents
@softwareversion
Preprints, Working Papers, ...
2023
Journal articles
Books
Book sections
Conference papers
Preprints, Working Papers, ...
2022
Journal articles
Conference papers
Master thesis
Other documents
Preprints, Working Papers, ...
Georg Loho, Mateusz Skomra. Signed tropical halfspaces and convexity. 2022. ⟨hal-03765509⟩
2021
Conference papers
Preprints, Working Papers, ...
Corbinian Schlosser, Milan Korda. Sparsity structures for Koopman operators. 2023. ⟨hal-04174190⟩
2020
Journal articles
Preprints, Working Papers, ...
International
Editorial activities
Series on Optimization and Its Applications, World Scientific (Jean-Bernard Lasserre)
AE SIAM J on Optimization (Didier Henrion)
AE Mathematics of Controls, Signals and Systems (Didier Henrion)
IFAC TC Robust Control (Didier Henrion)
IEEE-CSS TC RoCS (Didier Henrion)
National
Vice-Chair of the Scientific Committee on Foundations of Numerics for the French National Research Agency ANR 2021-2022 (Didier Henrion)
Member of the Scientific Board of the International Center of Mathematics and Computer Science in Toulouse 2019-2022 (Didier Henrion)
ANITI chair Polynomial optimization for machine learning 2019-2023 (Senior chair: Jean-Bernard Lasserre, Junior chair members: Milan Korda and Victor Magron)
SMAI-MODE Committee 2018-2022 (Victor Magron)
Math-Info Toulouse seminar organizer (Mateusz Skomra)
SPOT Toulouse optimization seminar, organization committee (Victor Magron)
BrainPOP Brainstorming days on measure and polynomial optimization, organization committee (Milan Korda)
Awards
CNRS Bronze medal (Didier Henrion 2004 and Victor Magron 2023)
Lagrange Prize in Continuous Optimization (Jean-Bernard Lasserre 2009)
ERC-Advanced Grant TAMING project (Jean-Bernard Lasserre 2014)
L. Khachyan Prize for lifetime achievement, Optimization Society of INFORMS (Jean-Bernard Lasserre 2015)
John von Neumann Theory Prize INFORMS Society (Jean-Bernard Lasserre 2015)
Invited Speaker at International Congress of Mathematicians 2018, Rio de Janeiro, Brasil (Jean-Bernard Lasserre 2018)
Grand Prix INRIA-Académie des Sciences (Jean-Bernard Lasserre 2021)
The team members have been implementing several software packages with open-source tools, released under free licenses. Advantages of this policy include the free access to source-code information, collaboration across academic partners without compromising the design of quality software and content for peer-reviewing. We present below a non-exhaustive list of these software libraries.
Numerical software
GloptiPoly3: Moments, optimization and semidefinite programming. Matlab parser for generalized problems of moments. Allows to build and solve convex linear matrix inequality (LMI) relaxations of the (generally non-convex) global optimization problem of minimizing a multi-variable polynomial function subject to polynomial inequality, equality or integer constraints. Can be freely downloaded and used. Developed by/with the help of: Didier Henrion, Jean-Bernard Lasserre and Johan Löfberg (Linköping University).
TSSOS: This is an open source Julia library developed for large-scale polynomial optimization, based on the sparsity adapted moment-SOS hierarchies. Related modules can perform complex polynomial optimization, eigenvalue/trace optimization of noncommutative polynomials, compute joint spectral radii for stability analysis, approximate attractors and invariants of sparse dynamical systems. Developed by/with the help of: Victor Magron, Jie Wang (Chinese Academy of Sciences, Beijing).
Validated computing software
We propose efficient numerical routines together with sure and reasonably tight error bounds. Applications include computer aided proofs, certification of numerical results in safety-critical control systems (e.g. cyber-physical systems).
RealCertify: Maple package to tackle the problem of deciding the non-negativity of rational polynomials over semi-algebraic domains defined by polynomial constraints with rational coefficients.
This is done by computing sum of squares certificates of non-negativity for inputs where such certificates hold over the rational numbers.
It can be applied to numerous problems coming from engineering sciences, program verification and cyber-physical systems.
It is based on hybrid symbolic-numeric algorithms relying on semi-definite programming. Developed by/with the help of: Victor Magron, Mohab Safey El Din (Sorbonne University).
SPECTRA: a Maple library which aims at finding at least one point in a spectrahedron, using exact arithmetic. SPECTRA should be used for small-dimension problems. It should not be considered as a competitor to numerical algorithms such as interior-point methods for semidefinite programming (SDP).
Contrary to numerical algorithms which are based on approximate computations and floating point arithmetic, SPECTRA is exclusively based on computations with exact arithmetic, and hence it should be primarily used either in potentially degenerate situations, for example when it is expected that the spectrahedron has empty interior, or when a rigorous certificate of infeasibility or feasibility is required.
Developed by/with the help of: Didier Henrion, Simone Naldi (XLIM Limoges), Mohab Safey El Din (Sorbonne University).
THESIS / HDR
2023
Corbinian Schlosser, Thèse: Parcimonie et optimisation convexe pour les systèmes dynamiques
2022
2021
DEPARTMENT
Jobs / Interships
REJOINDRE
Notre équipe de recherche
Pour plus d’informations sur les offres d’emploi, vous pouvez contacter