A Combinatorial Optimization Problem (COP) consists in the search for a solution in a discrete set (the feasible set) such that a (possibly multidimensional) function is optimized, the team contributions can be classified according to the considered specification of the feasible set. One of the team objectives is to study the structural properties of problems belonging to the categories below so as to, in fine, provide efficient tools to solve them optimally. In practice, the problems encountered often integrate two or more subproblems, such as integrated production scheduling and transportation problems. The ROC team carries out researches in the following COP:

Scheduling energy consuming jobs on parallel machines

Scheduling Problems

The feasible set is a set of schedules given by the ad-hoc specification of how a set of tasks can be positioned in time under temporal constraints (precedences, release dates, deadlines) and, possibly, using limited resources. The team considers various scheduling contexts (machine scheduling, resource-constrained project scheduling) and objectives (makespan, maximum lateness, fairness, total completion times). The team proposes resource constraint propagation algorithms, compact and extended MILP formulations, metaheuristics as well as complexity studies and dedicated solution algorithms. A special focus is also given on robust and multi-agent scheduling problems.

Some publications on scheduling problems

Reflector allocation and beam positionning for telecom satellites

Resource allocation problems

The feasible set is an assignment of resources to tasks without the scheduling part of the task, or with an already fixed scheduling. The objective is to minimize an assignment cost function subject to various constraints. This includes frequency assignment problems, employee timetabling, production planning, energy assignment, knapsack-like problems... The team mainly considers solution approaches based on CSPs and/or MILP formulations. Hybrid methods are also developed for solving complex integrated resource allocation and scheduling problems.

Some publications on resource allocation problems

Vehicle routing and transportation and network design problems

The feasible set is a set of vehicle routes satisfying different constraints on capacity, length, shape, time windows, etc. Besides time/distance classical objectives, the team considers other objectives, possibly in a multiobjective context, for example linked to multimodality, equity, energy consumption. The team considers MILP approaches, branch-and-cut-and-price techniques, Benders approaches, dynamic discretization methods and metaheuristics.

Some publications on vehicle routing problems

Combinatorial optimization under uncertainty

In the real world, the problem parameters are subject to uncertainty. While there are multiple ways of modeling and tackling uncertainty, the team has focused on reactive optimization (which aims at coordinating the iterative solution of deterministic problems through rolling horizons or repairing procedures) and robust optimization, in which uncertainty is modeled through a set of scenarios (each scenario corresponding to a fixed set of parameters) and for which a worst-case objective function over the set of scenarios is used to evaluate a set of decisions. The team proposes solution methods for robust scheduling problems for instance where task processing times are only known as intervals. Two-stage stochastic/robust approaches based on flexible scheduling structures are also proposed.

Some publications on robust combinatorial optimization

Structural properties, complexity and approximation guarantees

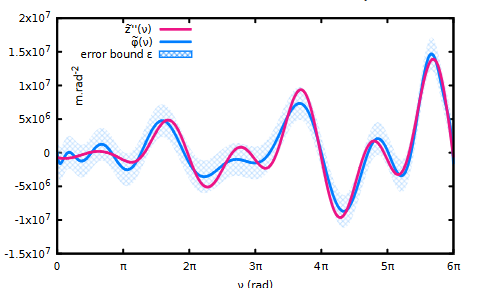
We carry out research to establish structural properties and performance-guaranteed approximations of combinatorial optimization and other computing problems. This include complexity and approximability analysis, polyhedral studies, theoretical comparisons of linearization schemes, piecewise linear bounding of non-linear functions and polynomial approximations for validated computing.

Some publications on complexity, polyhedral studies and approximations with error bounds

Combinatorial Optimization Problems in Machine Learning

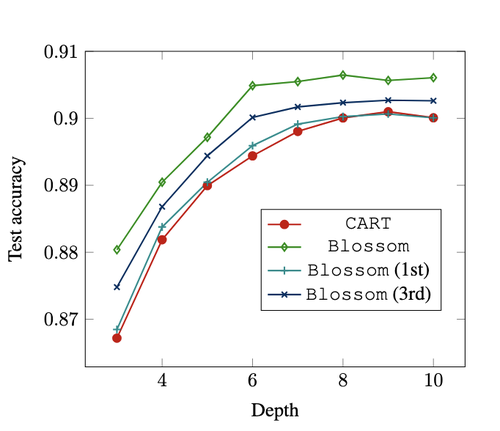
This works aims at improving machine learning techniques with the help of combinatorial optimization. Optimization techniques such as integer linear programming, constraint programming, maximum satisfiability, robust optimization are used to improve accuracy, privacy and fairness of ML models such as decision trees, ensemble models, etc.

Some ROC publications on optimization and learning