Optimization under uncertainty
The parameters of an optimization problems are often subject to uncertainties of all kinds. The team is interested in robust combinatorial optimization problems, especially scheduling problems under uncertainty. One avenue of research consists in proposing flexible solution structures for the proactive consideration of disruption by facilitating the repairing of computed solutions, notably by predetermining the feasibility of permutations within task sequences. The teams also contributes to advances in robust discrete optimization for scheduling
Robust combinatorial optimization
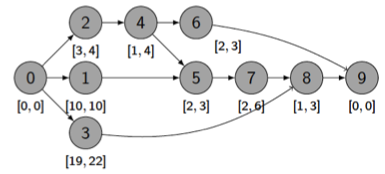
Project scheduling under interval uncertainty
In the real world, the problem parameters are subject to uncertainty. While there are multiple ways of modeling and tackling uncertainty, the team has focused on reactive optimization (which aims at coordinating the iterative solution of deterministic problems through rolling horizons or repairing procedures) and robust optimization, in which uncertainty is modeled through a set of scenarios (each scenario corresponding to a fixed set of parameters) and for which a worst-case objective function over the set of scenarios is used to evaluate a set of decisions. The team proposes solution methods for robust scheduling problems where task processing times are only known as intervals.
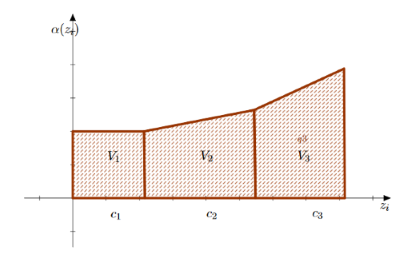
Cycle time of a cyclic job-shop problem under interval uncertainty as a cycle polytope volume
Robustness studies are also conducted in the supply chain tactical planning problem and in the spatial domain for robust guidance problems.