Computational Methods
We contribute to the design of efficient solving methods for hard combinatorial optimization problems. In particular, we design algorithms and models for constraint programming, mixed-integer linear programming and hybrid approaches.
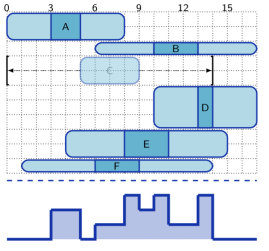
Propagation of the cumulative constraint
Constraint Programming
The description of the feasible set follows the general CSP framework involving variables, domains, and constraints. The objectives are usually transformed in constraint(s). The team proposes efficient constraint propagation algorithms and intelligent tree search methods based on learning and SAT-inspired techniques.
Some publications on Constraint Programming
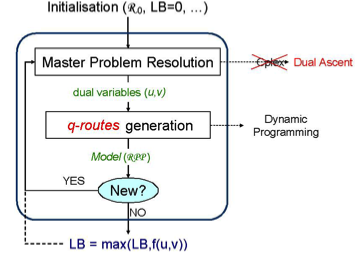
Column generation based on q-routes for vehicle routing
Mixed Integer linear programming
The feasible set and objective(s) involve only linear expressions on integer or fractional variables. In this domain, the team carries out researches on branch-and-cut, branch-and-price and more generally decomposition methods.
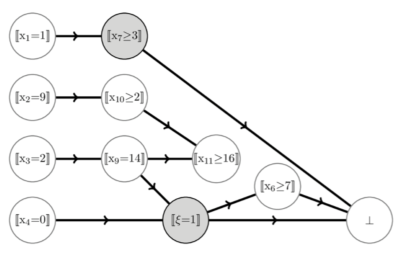
Implication graph in an hybrid CP/SAT Solver
Hybrid methods for combinatorial optimization
Combining different approaches is often the key in significant computational breakthrough for combinatorial optimization. The teams carries out research in different hybridizations between several components among Mixed-Integer Linear and Non-Linear programming, Constraint Programming, Dynamic Programming, Boolean Satisfiability, Local Search.
Some publications on hybrid methods
A flow-based heuristic for a multi-skill technician allocation and scheduling problem
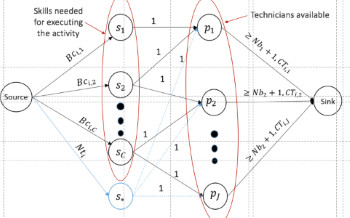
Dedicated Algorithms
Depending on the structure of the considered combinatorial optimization problem, the team also develops dedicated exact or approximated algorithms: specific heuristics, greedy algorithms, local search methods, dynamic programming, graph-based heuristics...